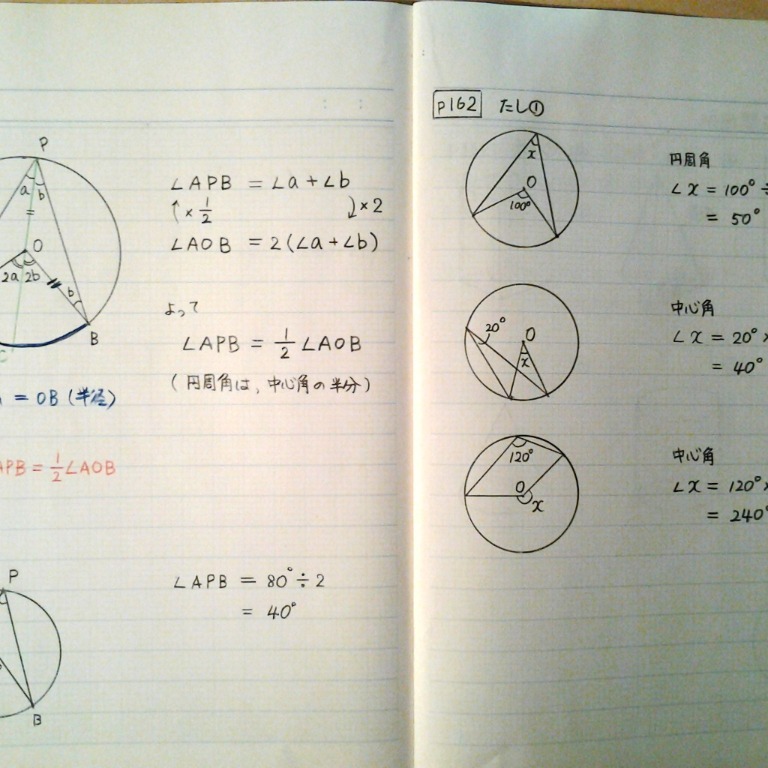
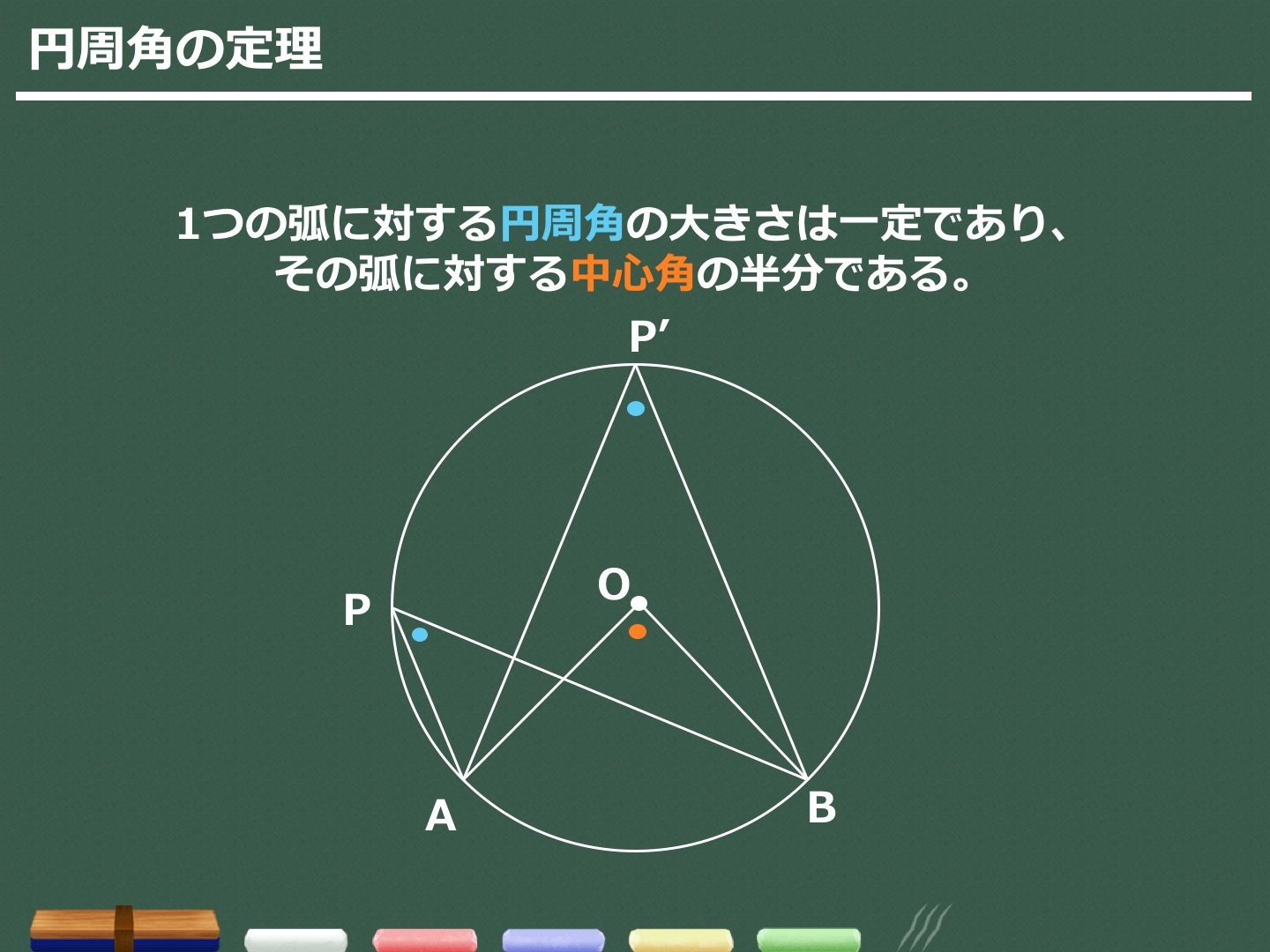
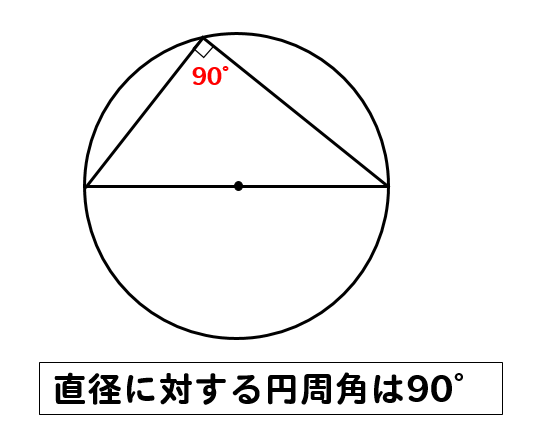
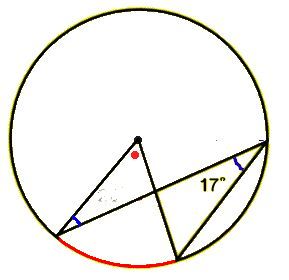
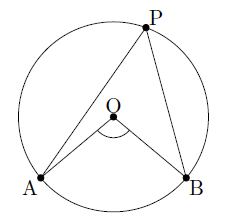
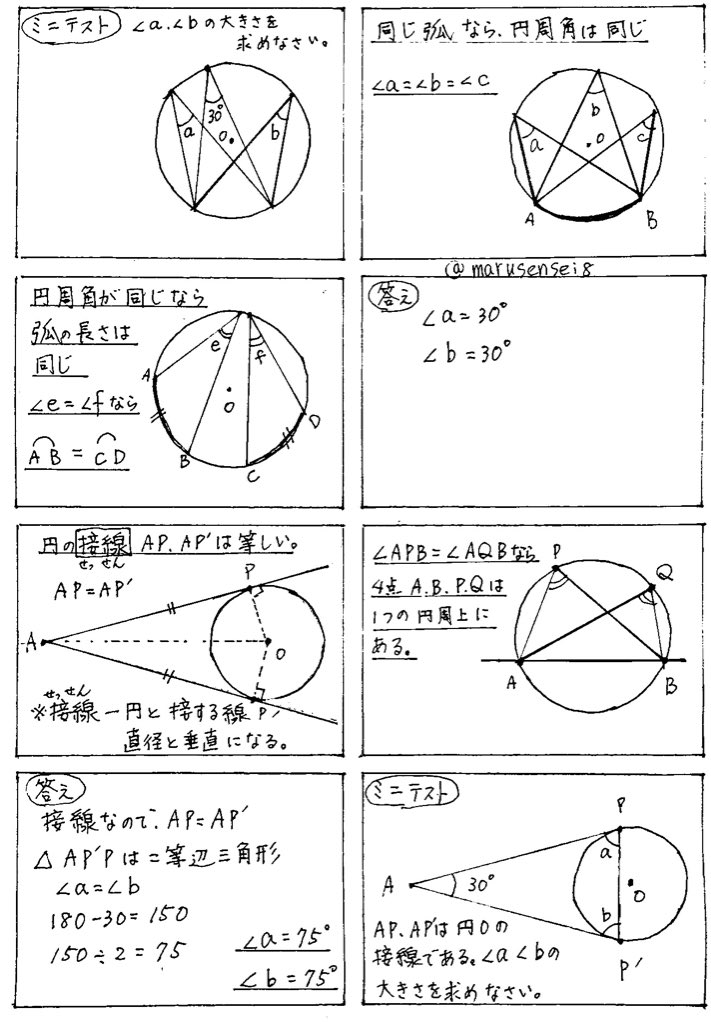
(1)円周角は中心角の半分なので (3)中心角は円周角の2倍なので (4)右の図のように、線分aoを引き二等辺三角形を 2つ作る。 c 二等辺三角形の底角は等しいので〇=° =45° 円周角と中心角の関係から b 解説 (1)直径に対する円周角なので,①円周角とは ②円周角と中心角の関係 到達目標 弧の長さと中心角が比例することを知る 円を人に説明するにはどうしたら良いでしょうか?三角形と円 三角形と円 円周角と中心角 定理 1つの弧に対する円周角は常に一定で、その弧に対する中心角の に等し い。 点Pを何処にとっても ∠APBの大きさは変わらない。 円周角は常に中心角の半

円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張
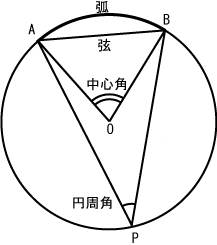
円周角と中心角の関係 弧
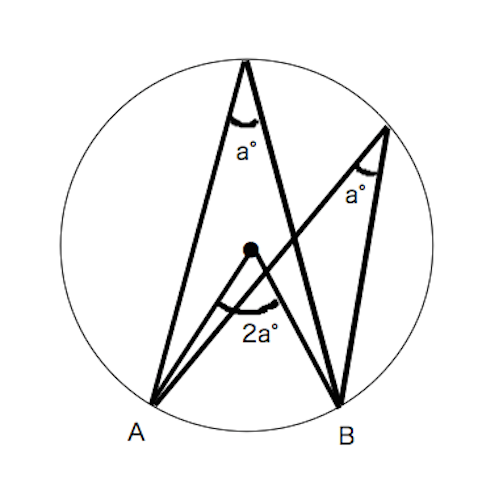
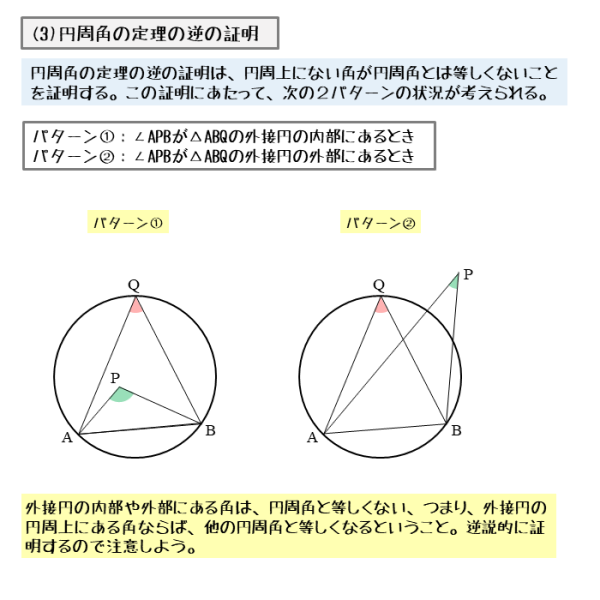
円周角と中心角の関係 弧-円周角の定理の証明。3つのパターンから分かる円周角と中心角の関係性|アタリマエ! 🤞 等しい円周角に対する弧は等しい• 上の図でいくと、2本の線が出ている2点を結んだ場所です。円周角と中心角に関心をもち、それらの関係や性質を見い出したり、その証明にどのような図 形の性質が用いられているのかを考えたりしようとしている。 数学への関心・意欲・ 態度 (2)円周角と中心角の関係や 、



円周角
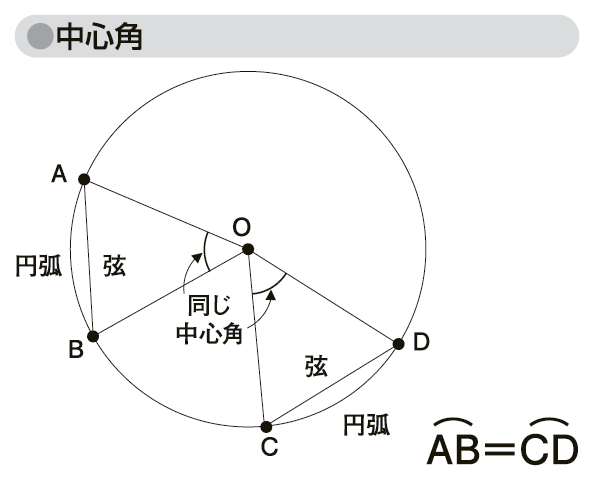
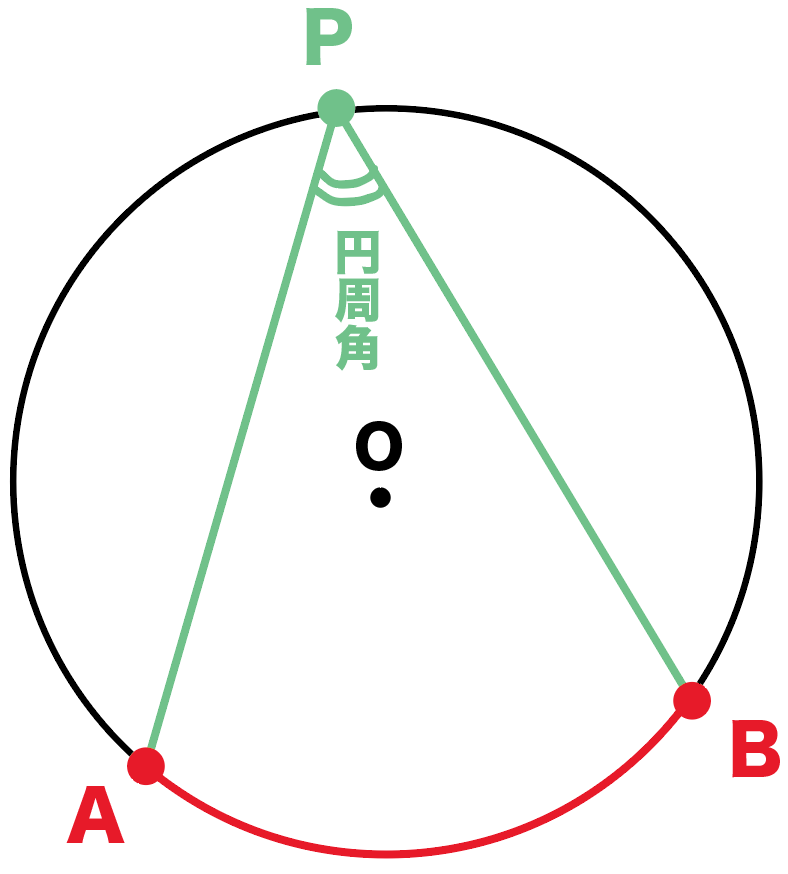
中心角92°が書いてあって,円周角が書いてないときは,92°÷2= 46° で円周角が求まります. 円周角46°が書いてあって,中心角が書いてないときは,46°×2= 92° で中心角が求まります.円周角の定理を予想することができる。 円周角と中心角の位置関係を3つの場合に分け,円周角の定理を証明することが できる。 (3) 準備 ①学習プリント ②分度器 ③パソコン④学習ソフト図形ランチボックスVer2(創育)円周上に2点A,Bをとると、 「弧AB」 ができるよね。 そして、 円の中心O と点A,Bをそれぞれ結んだときの∠AOBを 「中心角」 と言うよ。
円周角と中心角(2) 1 1つの弧に対する円周角は、すべて等しい。 Q P A B (1) (2) 次の図で、∠xの大きさを求めなさい。 362 35° x 28° x (3) (4) (5) 65° x 24° O x (6) 60° O x 1° 35° 46° y x 36° 52° 80° x 100° 30° 2 次の図で、∠x、∠yの大きさを求めなさい。 80° 35° 54° =22ア 円周角と中心角の関係の意味を理解し、それが証明できることを知ること。 イ 円周角と中心角の関係を具体的な場面で活用すること。 円周角の定理については、記されておらず、「円周角と中心角の関係」に留められている。円周角 三角形の外角の関係を使う問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 三角形の外角は それと隣り合わない2つの内角の和に等しい。
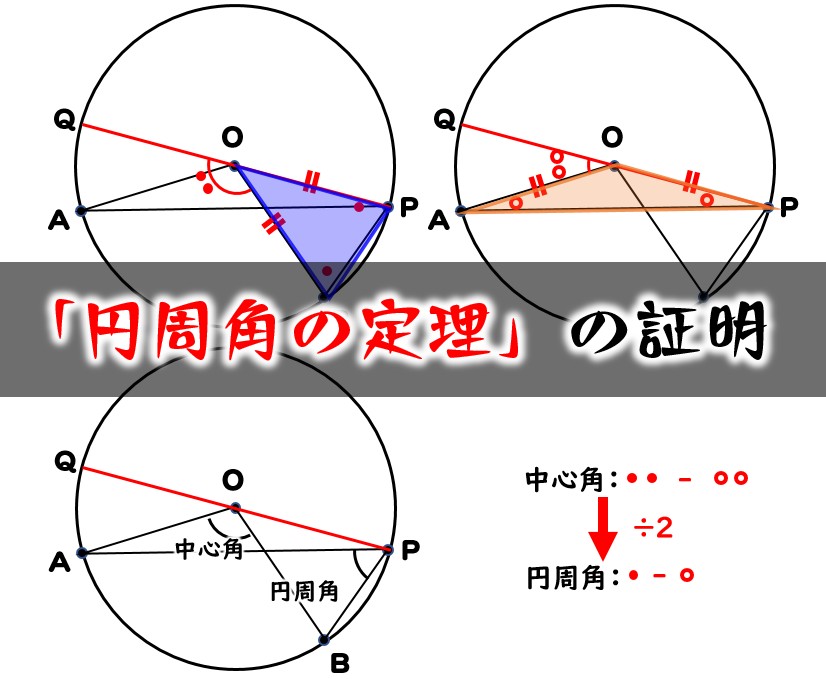
Xは3コマ分の中心角の半分 (=円周角) → x = 1 2 (3×45°) = 135 ° 2 = 675° 円周角の定理の証明② 中心を含むとき 次は以下のように、「ある1点から円周上の2点に伸ばした2直線の間に、中心が位置するとき」です。 三角形abc中に中心oが来るイメージです。 このとき、円周角の定理を証明するには、 ∠bac=½ ∠boc1区画分の円周角の大きさは30°となります。 6等分の場合 1区画分の中心角は60°、円周角は30° これを利用しながら問題を考えていきます。 補助線を1本引いて、1区画分の円周角の大きさを求めます。
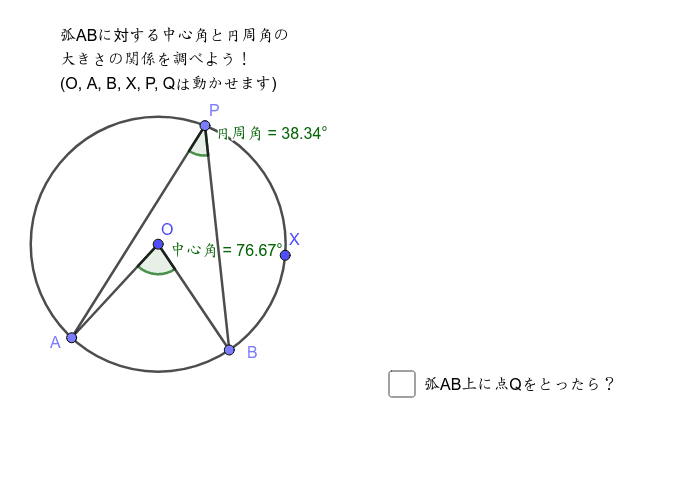



円周角の定理 Geogebra



あなたは3秒で解けますか ビジネスに役立つ論理思考を 中学数学 で鍛える Sbcr Online
2 円周角と中心角 また, は,円oの弦abに対する円周角を∠apbとすると 弦abは直径 ∠aob=180°∠apb=90° が成り立つことから導けます。 それでは,例題を通して,円周角と中心角の関係などを確認してみましょう。1 実験を通して,円周角と中心角の性質にア-①観察 ついて考える。(本時)自己評価カード ワークシート 2 二等辺三角形の性質から,円周角と中心イ-①自己評価カード 角の関係について考察し,証明する。ウ-①ワークシート ポストテスト円周角と中心角の関係については, 二等辺三角形の底角が等しいことと,三角形の一つの外角がそれと隣り合わない2 つの内角の和に等しいことを使えば証明することができる。生徒にとって証明の必要性や良さを感じ取るためには, 今まで知らなかったことや,疑わしいことを証明で解明し, その正しさを明らかにできることを体験することが重要である。 本単元は,証明のよさを理解すること
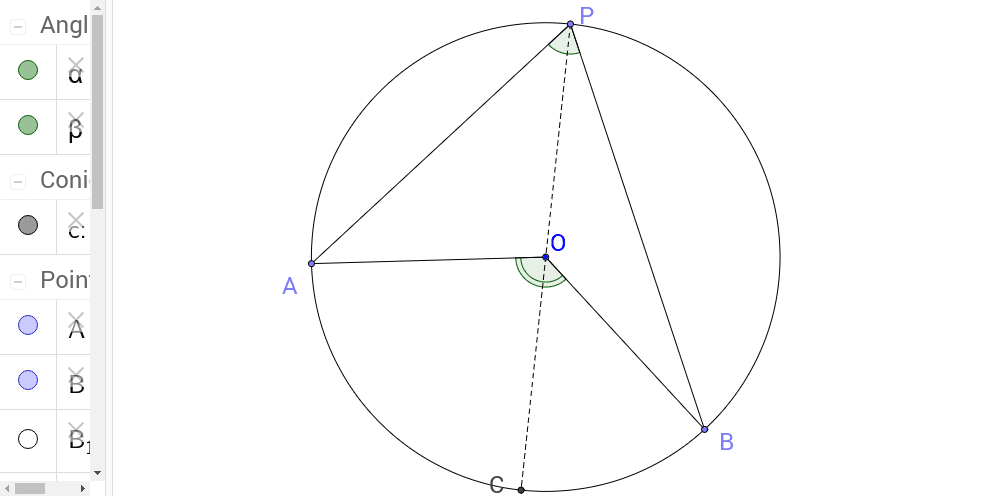



中心角と円周角 Geogebra




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学
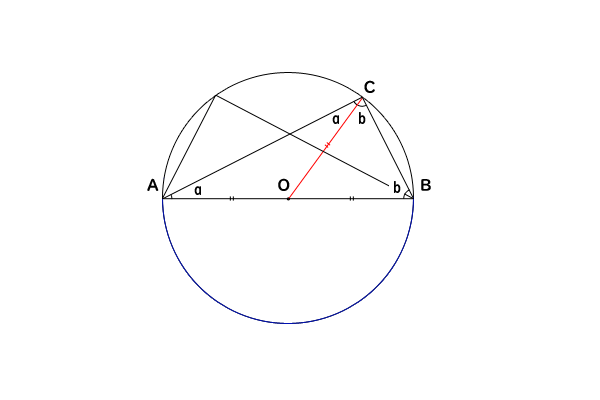
円周角1 円 円とは定点oから 一定の距離rにある点の集合 である。 このときの定点oを 円の中心 といい、距離rが 円の半径 である。 この定義を言い換えると、 「半径はどこでも等しい」 となる。 半径はどこでも等しいので、2つの半径oa, obと弦abによってできる三角形は必ず二等辺三角形である。の2つの円周角の定理があるんだ。 どっちも、 「同じ弧に対する」 っていう条件が含まれてることに注意ね。 定理1 「円周角は中心角の半分」④円周角と中心角の関係 を用いて考えた結果が適 切であるかどうかを振り 返って確かめることがで きる。 ①円周角と中心角の関係 や、同じ弧に対する円周 角の性質などを記号を用 いて表したり、その意味 を読み取ったりすること ができる。 ②円周角
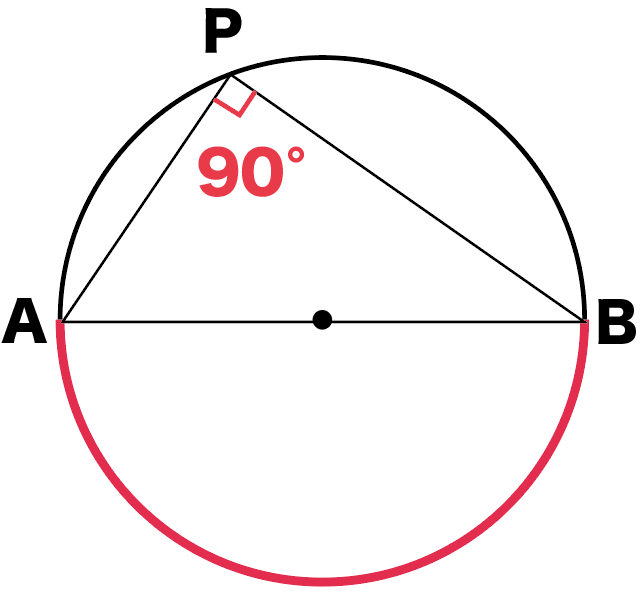



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
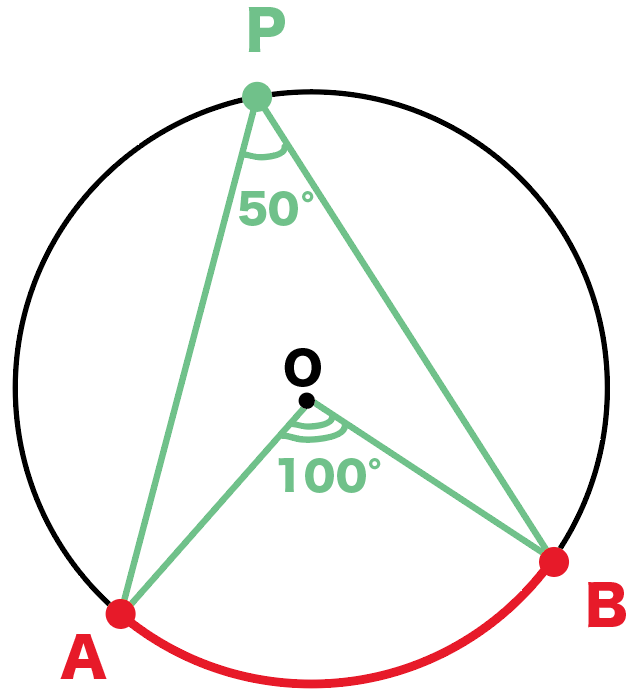
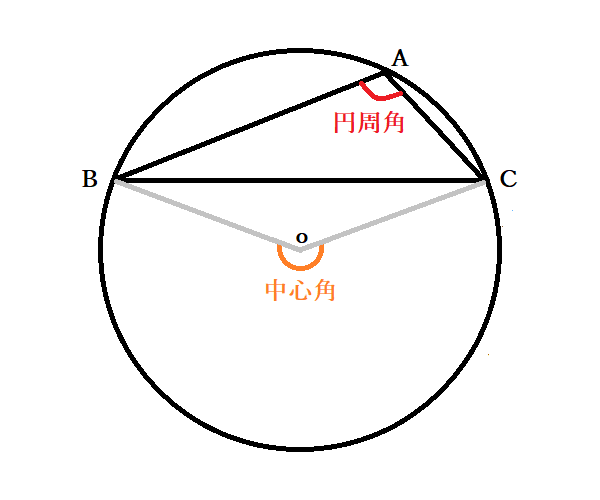
円周角の定理では中心角が頻繁に利用されます。 この理由として、円周角と中心角は以下の関係があるからです。 円周角 × 2 = 中心角 例えば円周角が30°の場合、中心角は必ず60°です。 円周角を二倍すれば中心角の角度になります。 一方で中心角が80R⑦ 1つの弧に対する中心角と円周角の関係を説明できる。 ⑧ 予想した円に内接する四角形の性質について、仮定と結論に分けることができる。 R⑨ 仮定と結論の意味を説明できる。 ⑩ 予想した性質の中でまだ証明されていない性質は、「円に内接する四角 円周角が ● ∠ A P B = ● 中心角が ● ∠ A O B = 2 × ●



円周角 中心角 時事用語事典 情報 知識 オピニオン Imidas イミダス



円周角 中心角 時事用語事典 情報 知識 オピニオン Imidas イミダス
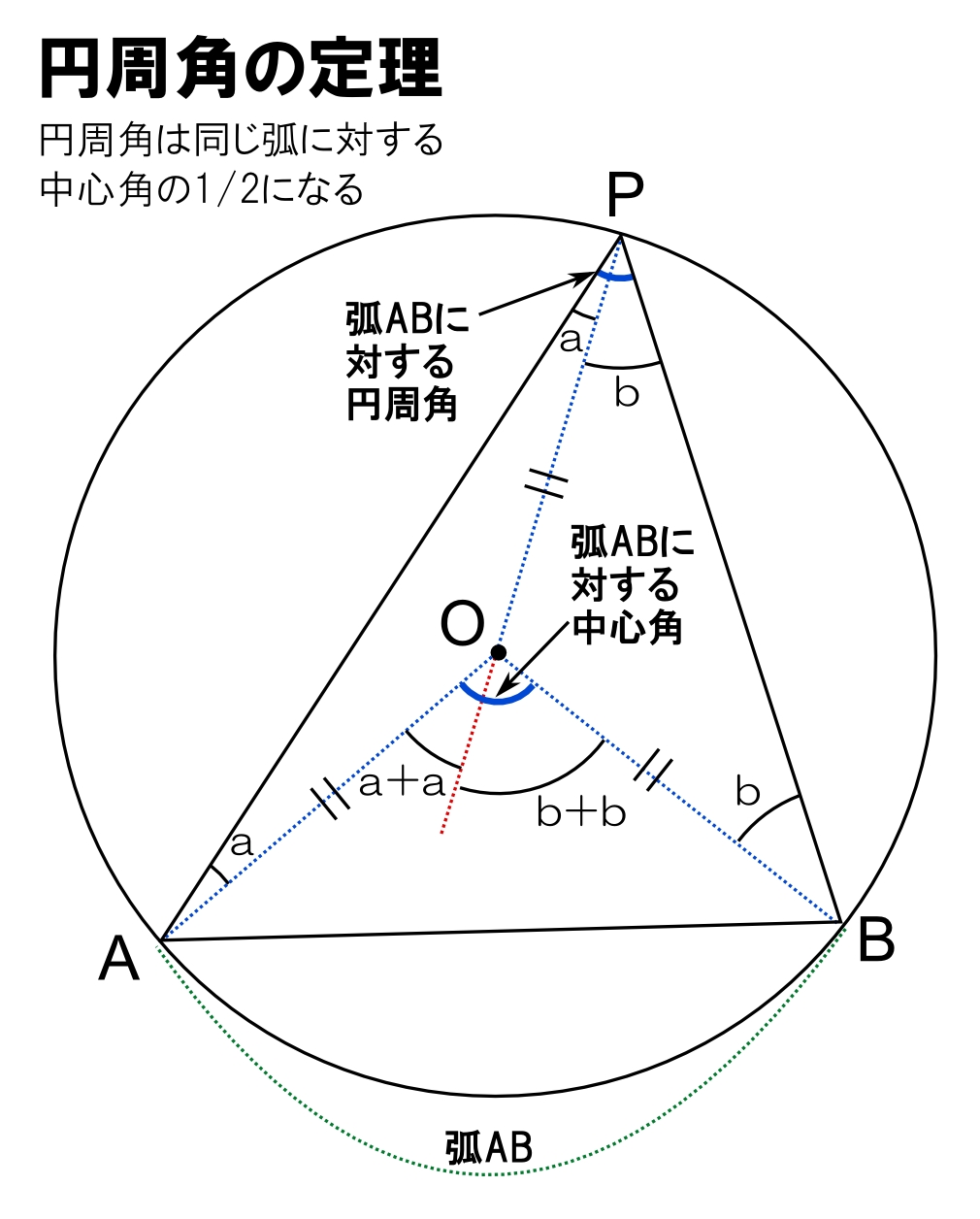
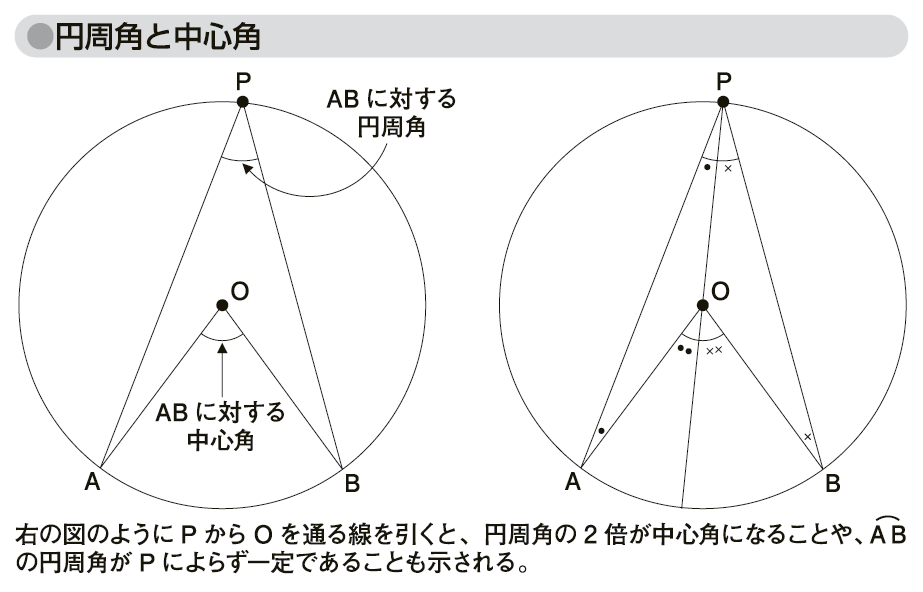
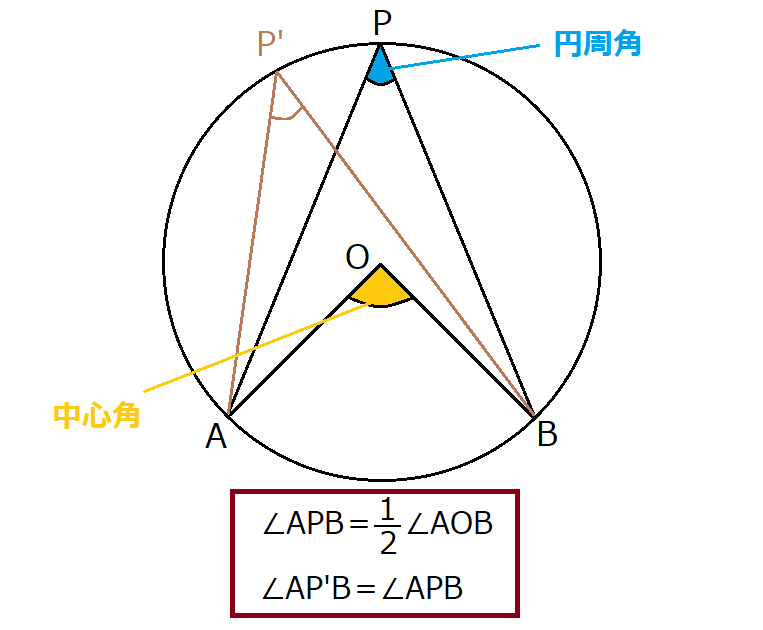
これは同じ円に2つの角を並べてみるとよくわかりますよ。 図からもわかる通り、角は3点から作られていますが、 中心角と円周角は2点が共通している ことがわかると思います。円周角が中心角の半分であることの説明 直線POが弧ABと交わるとき なぜ円周角は中心角の半分なのでしょうか。 下の図で説明をします。 \(po\) を通る直線を補助線としてひきます。 円 \(o\) の半径は1.円周角と中心角 ポイント:円周角,中心角を理解できる。 また 点Pの位置によって、どのように変わっていきますか。 (1) OPAで、OP=OAなので また OPAの外角の性質から 円周角= ×中心角 (2) 直径POKをひくと (1)より ③+④ 円周角= ×中心角



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく
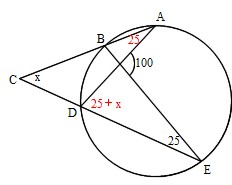



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
イ 円周角と中心角の関係を具体的な場面で活用すること。 <この教材で身に付けたい力> 円周角と中心角の関係を理解し,それを図形の性質の考察や計量に用いる能力を伸ばすととも に,図形について見通しをもって理論的に考察し表現する能力を伸ばす。2/3時 ・ 円周角の定理を使って、角の大きさを求めることができる。 ・ 円周角の定理を理解する。 前時の証明を読み、円周角と中心角の関係を確認する。 本時の学習内容「円周角の定理を使って、角の大きさを求めよう」を知る。 (ウ) の場合につい・図をもとに「円周角」を定義する。 2 動的幾何学ソフトウェア(GeoGebra)を使って,同じ弧に対する円周角や中心角との関係を予想する。 T1:点A,Bや点Pを動かすと,中心角や円周角の大きさが変化しますね。何か気がつくことはありますか。




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張



1
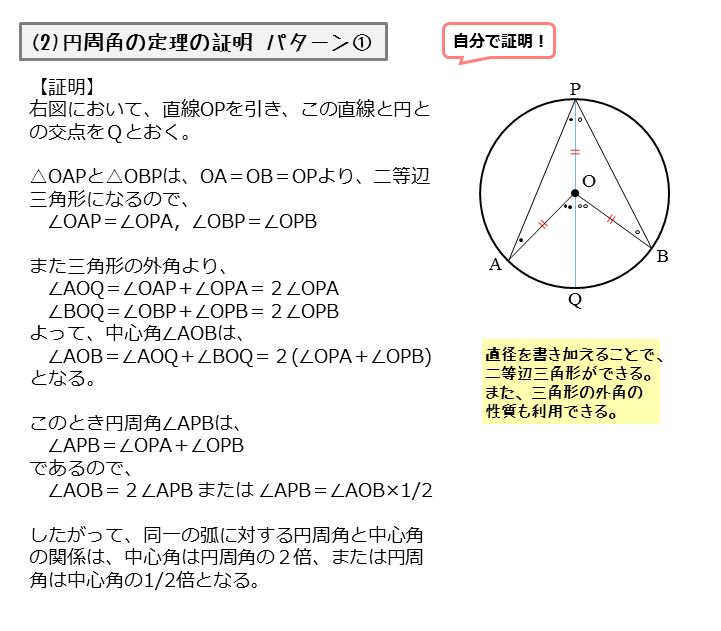
円周角と中心角の関係や、それを証明する方法を理解し、円周角の定理を活用する問題を繰り返し練習します。 円周角の定理(1) ⇒ 答え 円周角の定理(2) ⇒ 答え ⇒ 大問1の (2)の「円に内接する四角形の性質」を用いた場合の解説はこちら 円周角の(ア) opaで,op=oa(半径)だから,・・・・1 ∠aob=∠opa+∠oap(三角形の外角) 1,2より したがって ∠apb=1∠aob 2 円周角の定理の証明の3パターン 「円周角の定理」を証明していくぞ。 3点a・b・pがある円oを想像してくれよな。 円周角と中心角の位置関係はつぎの3通りある。 点 pがob上にあるとき;




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4




本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download
前提として、円周角と中心角の関係は証明完了しています。つまり 円周角 = 中心角 という式は使用可能です。素晴らしい。 この図の円周角2つはともに同じ中心角をもってます!そして繰り返しになりますが、以下の式は成り立ちます。 円周角 = 中心




中学数学 円周角 中心角



円周角と中心角 中学から数学だいすき




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
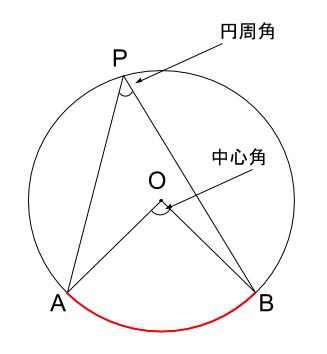



中学数学 円周角の定理 導入 中学数学の無料オンライン学習サイトchu Su




数学 中3 56 円周角の定理 基本編 Youtube
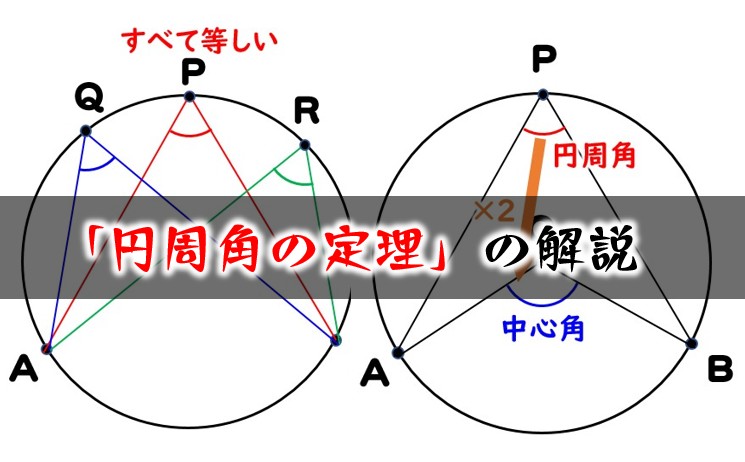



円周角の定理の解説 問題の解き方 数学fun




平面図形23 円周角の定理の逆 怜悧玲瓏 高校数学を天空から俯瞰する




中心角とか円周角とかどこがどこを指すのか分かりません Clear




中3数学 円周角 ブーメラン型四角形 まとめと問題
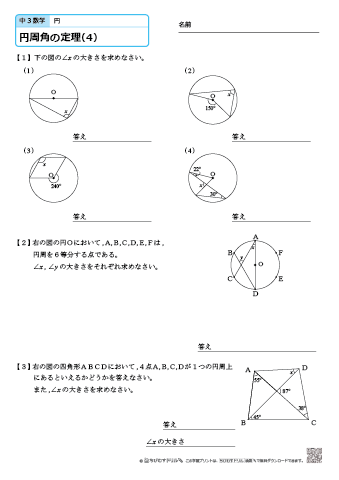



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



ファイル 中心角と円周角 Png Wikipedia



Tossランド 円周角の定理 円周角と中心角




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学



学習指導要領ナビ Jp 中学校 数学 第3学年の内容 b図形 円周角と中心角の関係



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ
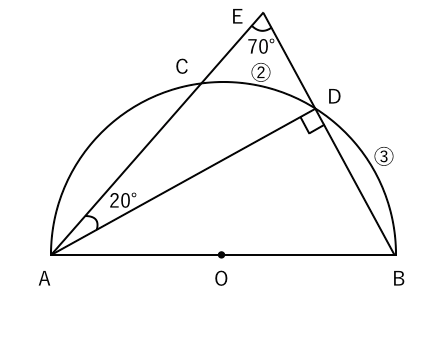



円周角と比の問題 苦手な数学を簡単に



1




円周角 三角形の外角の関係を使う問題



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
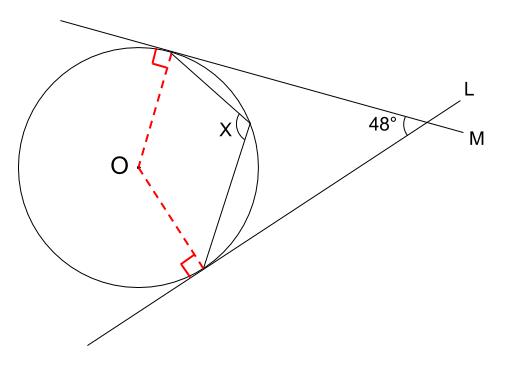



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円周角の定理 中学校学習指導要領および教科書の扱い 身勝手な主張
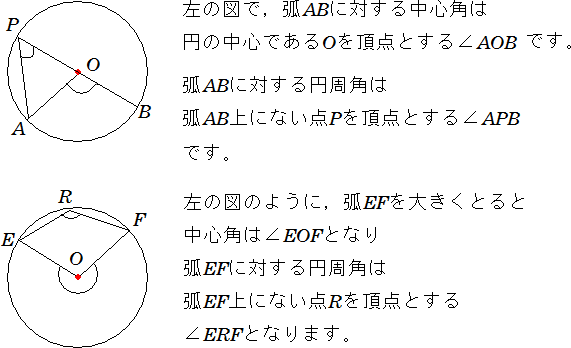



円 円周角と中心角について 中学数学 定期テスト対策サイト



同じ弧に対する円周角
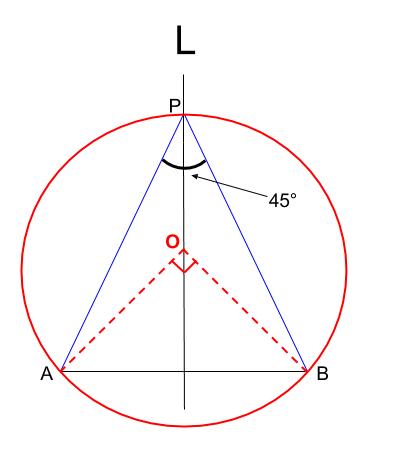



45 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su




数学 三角関数 円周角の定理の証明 Qiita



円周角



円周角の定理の応用で 弧の長さから円周角が分かったりその逆もありますが Yahoo 知恵袋



円周角の定理 On Vimeo
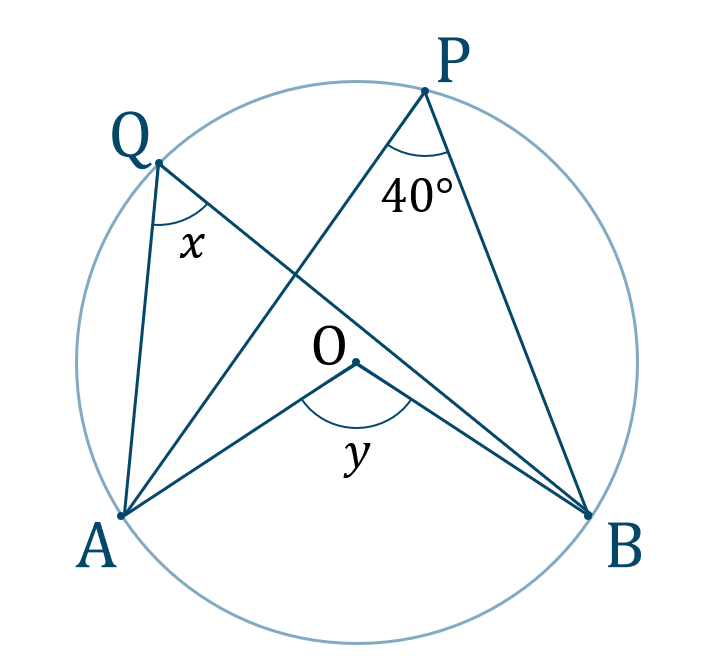



数学a 円周角と中心角の関係の使い方とコツ 教科書より詳しい高校数学




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
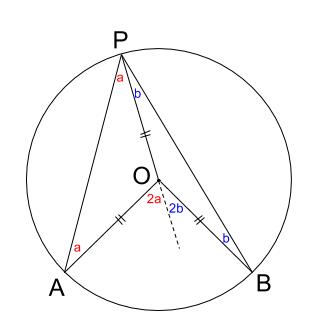



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube



1




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



中3数学 円の性質2 円周角と中心角 すべて無料 星組の中学数学講座
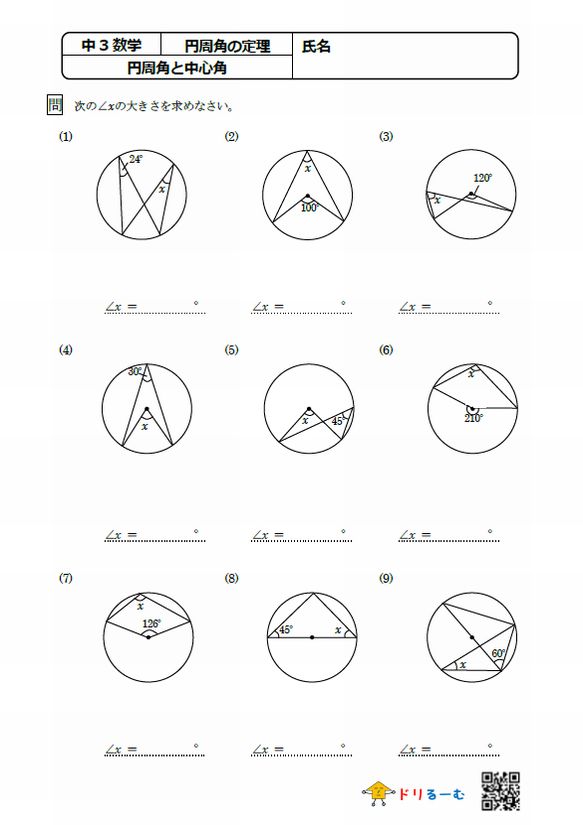



円周角と中心角 ドリるーむ



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



円周角の定理とその逆 思考力を鍛える数学



同じ弧に対する円周角




数学 中3 57 円周角の定理 少し応用編 Youtube



円周角
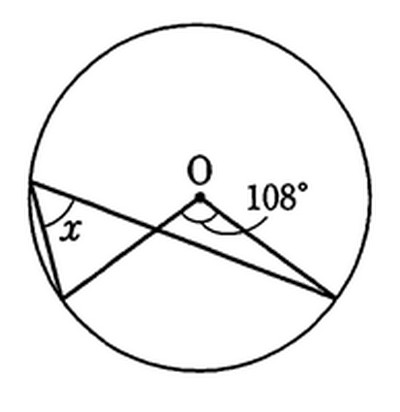



円周角の定理は人生の縮図 円周角の定理が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦
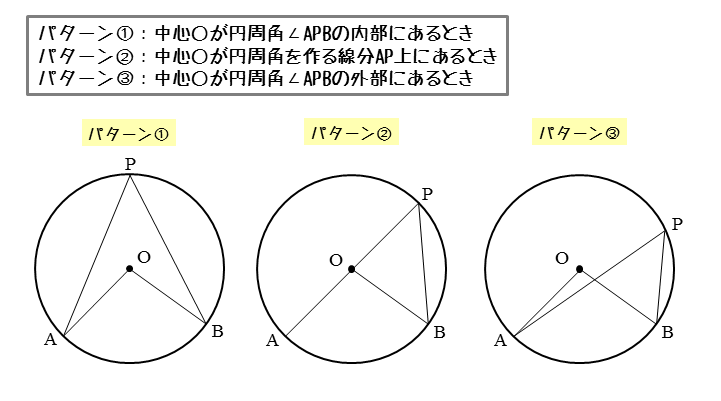



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円周角の定理とその逆の証明 高校数学マスター



円周角の定理の証明 図で分かりやすく解説 数学fun



円周角の定理 苦手な数学を簡単に




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



円周角の定理の証明を3つ紹介 逆も把握しよう ヒデオの情報管理部屋



中心角は円周角の2倍になる



円周角と中心角



円周角の定理



これで大丈夫 高校入試 円周角の必勝法 高校入試徹底対策ガイド




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく



同じ弧に対する円周角



1



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス



円周角と中心角 まなびの学園




本時のねらい 円周角と中心角の意味を理解し 二つの角の関係について 操作 実験を通して予測したことを確認し 定理としてまとめる Ppt Download




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
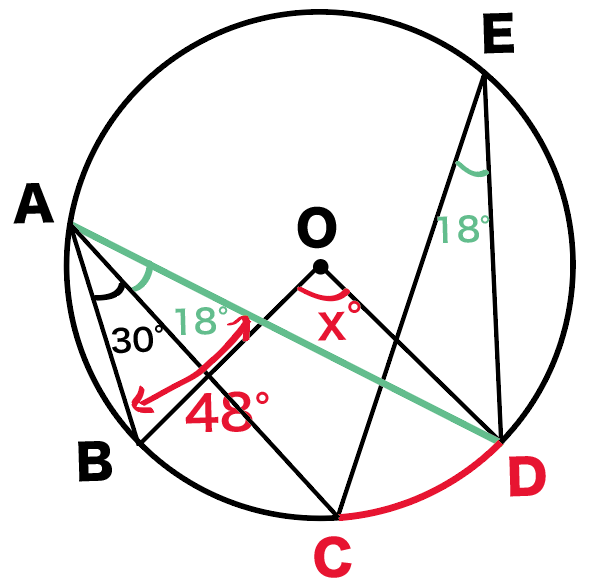



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
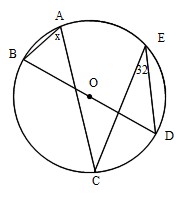



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円周角の問題 中学から数学だいすき




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
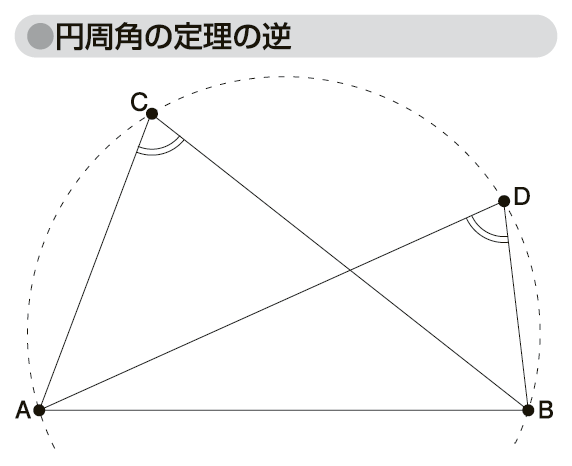



円周角 中心角 時事用語事典 情報 知識 オピニオン Imidas イミダス
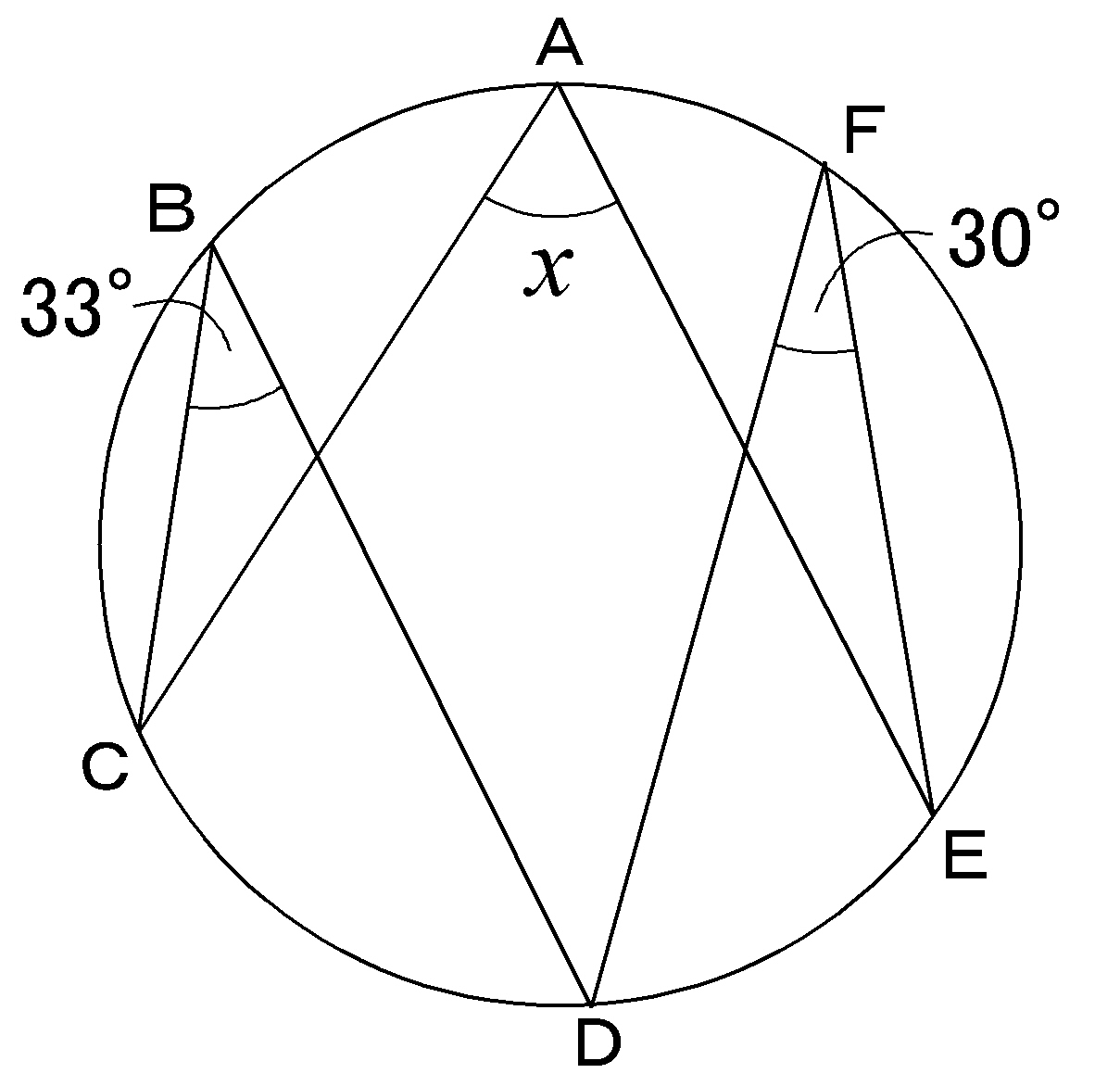



Wordで使える 円周角の問題の図 その2 Wordで数学問題プリントを作ろう
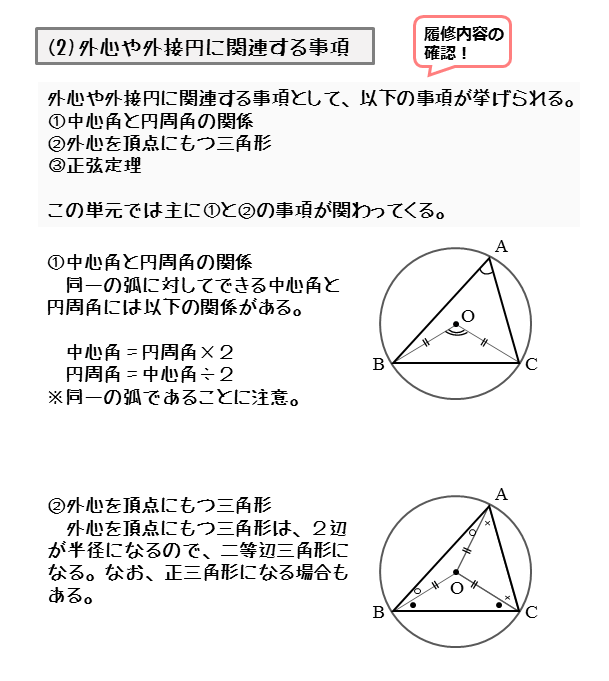



図形の性質 外心について 日々是鍛錬 ひびこれたんれん
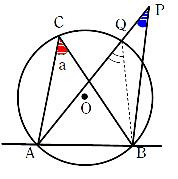



中学校数学 3年生 図形 円 Wikibooks
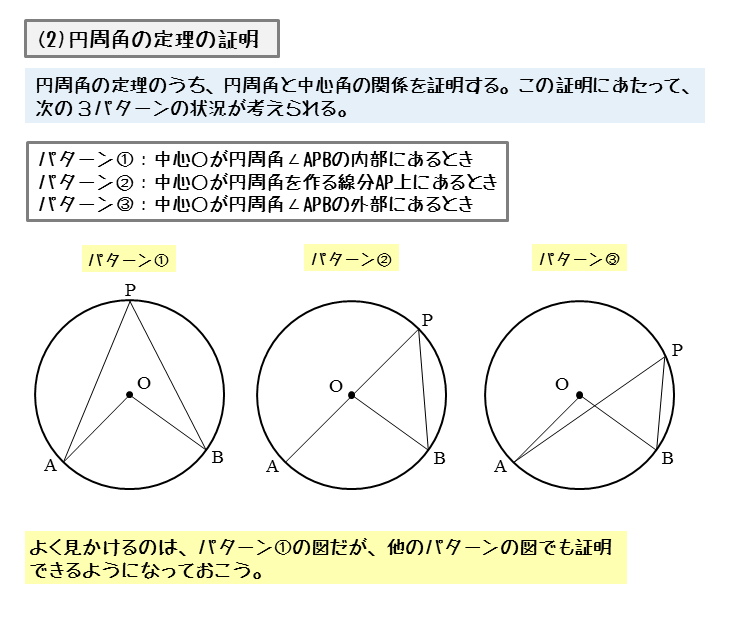



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



中心角



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典



円周角
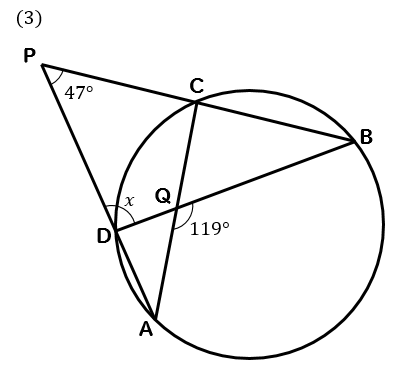



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




中3 数学 円周角の定理 中学生 数学のノート Clear
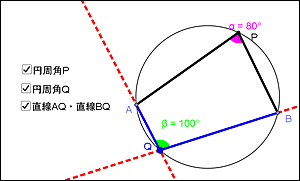



授業実践記録 数学 第3学年 数学的な見方 考え方を養う 円周角の定理 の授業 動的幾何学ソフトウェア Geogebra を用いて知識を拡張 統合する 啓林館
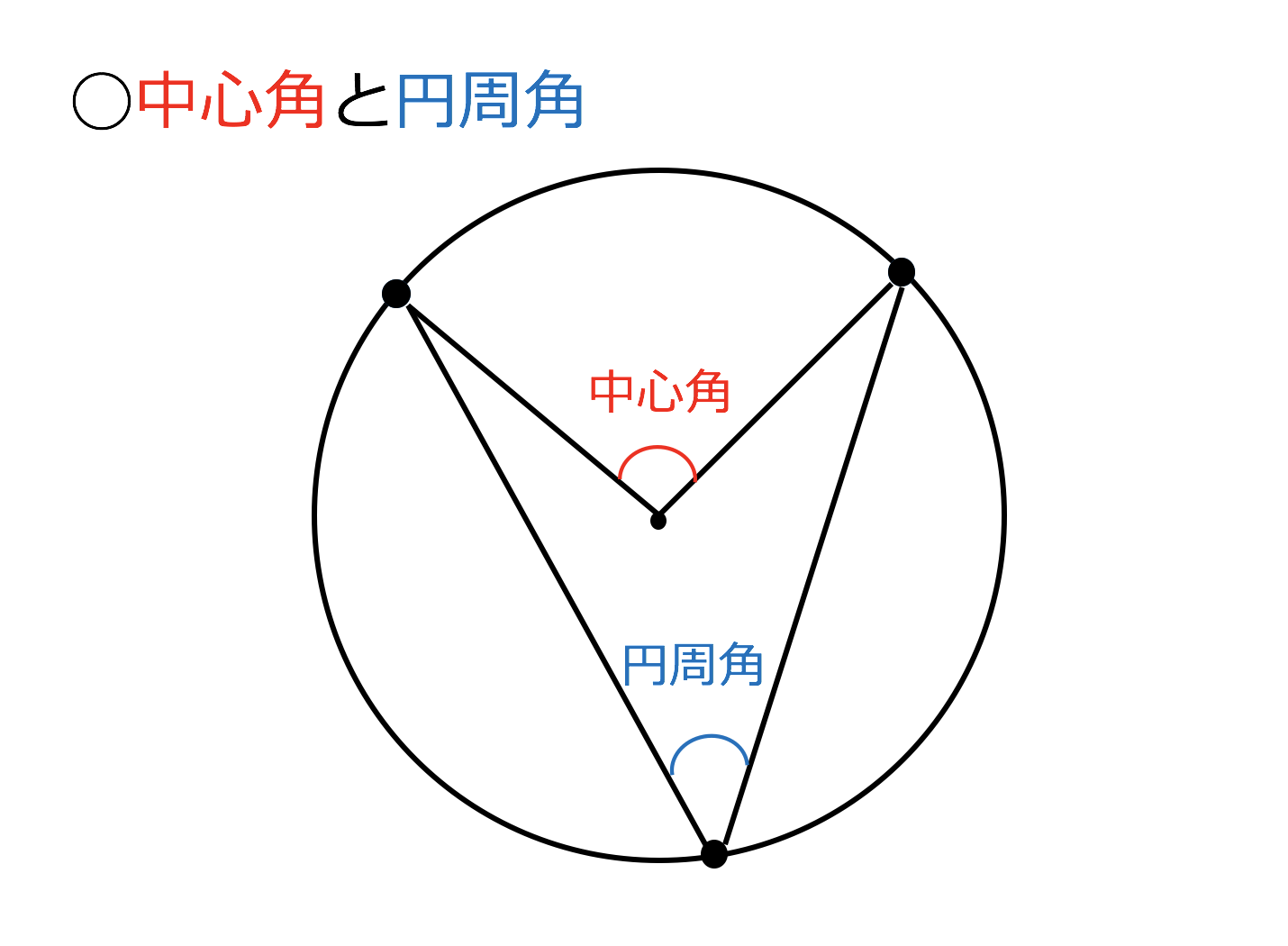



3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ




円周角の定理と中心角 中学3年数学 Youtube
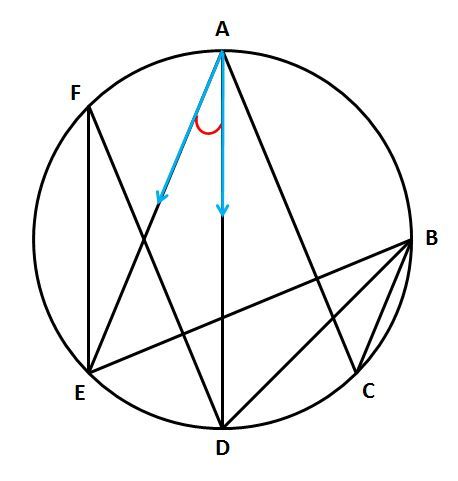



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




円周角の定理の基本 計算 無料で使える中学学習プリント



Studydoctor円周角の定理と中心角 中学3年数学 Studydoctor



0 件のコメント:
コメントを投稿