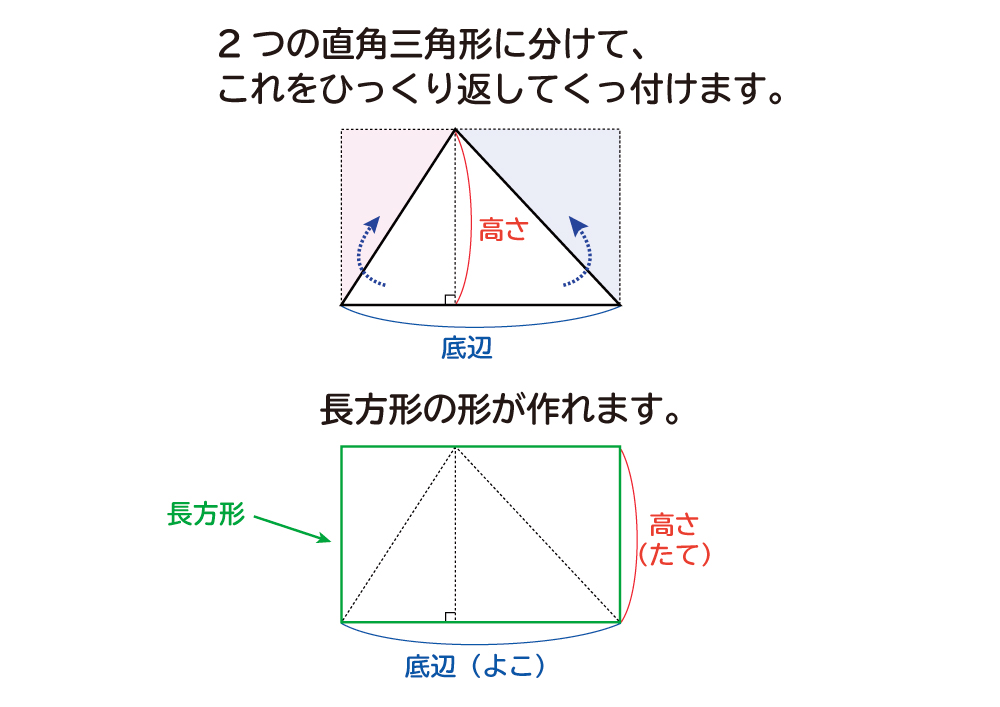
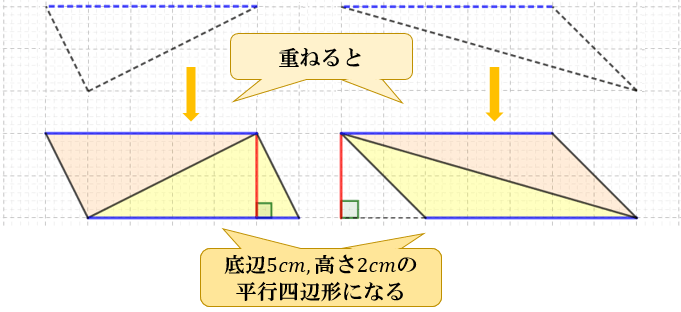
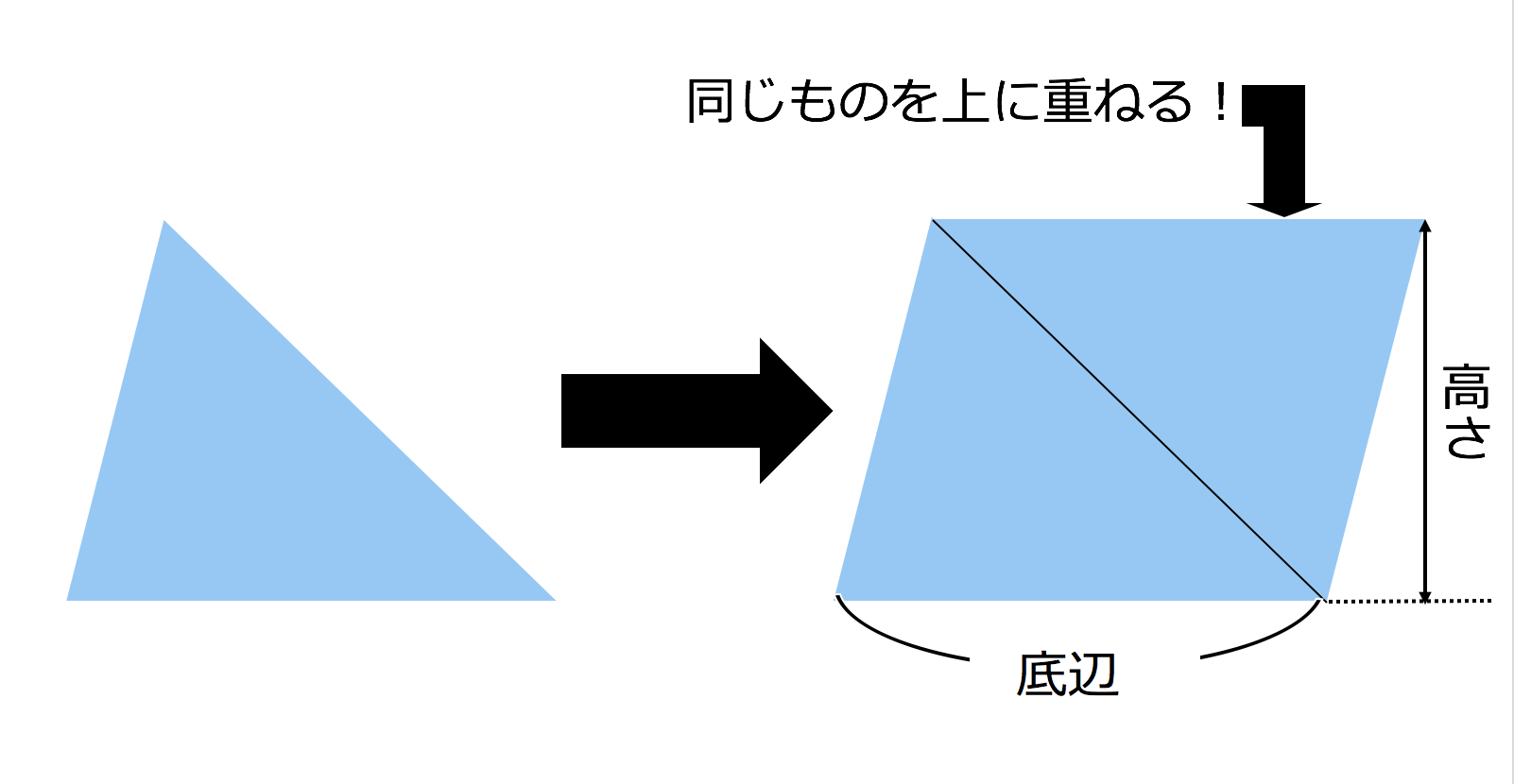
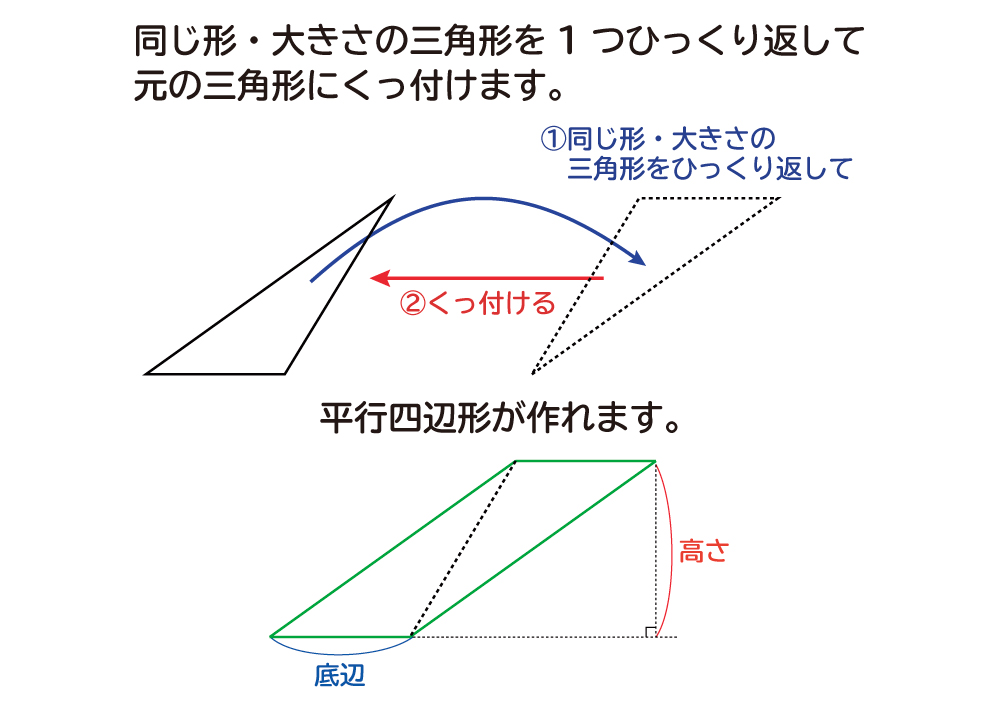
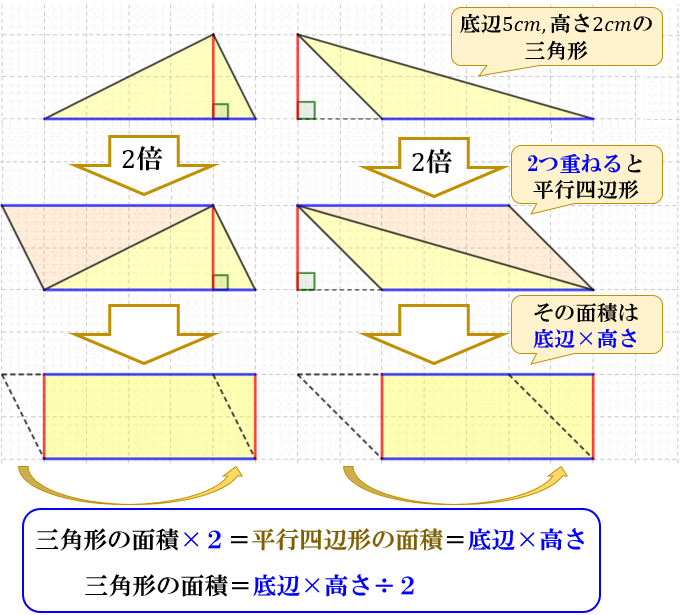
三角形だと底辺×高さ÷2なのに、台形だと上底+下底ってなるのか。 何年の学習指導要領で小中学校を過ごしてきたのだろう。 一時期台形の面積がなかった時期があったと記憶している。 台形を対角線で切り離す。面積は2つの 三角形の和だ。 (上底下底)×高さ÷2 = 上底×高さ÷2+下底×高右 図1 のような三角形の面積は、いずれも (底辺)×(高さ)÷2 で求められます。 次のように分数の形で書くこともできます。 (面積)= (底辺)×(高さ)2nnnnnnnnnnnnnnn (1) 2で割ることを忘れる答案が多いので注意しましょう。 右 図2 の三角形のS:底辺×高さ÷2です。 t:なぜそうなるのか説明できる? s:この三角形をひっくり返してくっつければ、平行四辺形になる。底辺×高さで面積が出て、2倍したから2で割れば三角形の面積が出る。 t:弟は感心してさらに聞いてきた。
Q Tbn And9gct71t318twmynw63dxmqoj5dsomuiz6o0rnzjk6hursgayaq9 L Usqp Cau
底辺×高さ÷2 なぜ
底辺×高さ÷2 なぜ-積分とは何か? 最もわかりやすく簡単に理解できるように解説 Tweet 積分とは、一言で表すと「ある関数が描く面積」であり「微分と正反対の演算」です。 そして積分を理解すると、ある関数の面積を、とても簡単に求められるようになるため、さまざま円錐の底面積=5×5×314=785cm 2 四角錐の底面積 四角錐の底面積は、四角柱の底面積と同じ計算です。 四角錐の底面積=(35)÷2×6=24cm 2 三角錐の底面積 三角錐の底面積は三角柱の底面積と計算式が同じです。 三角錐の底面積=10×2÷2=10cm 2




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
四角柱 ⇒ (上底下底)÷2×高さ 三角柱 ⇒ 底辺×高さ÷2 円錐 ⇒ 半径×半径×314 四角錐 ⇒ (上底下底)÷2×高さ 三角錐 ⇒ 底辺×高さ÷2 各図形の底面積の具体的な計算方法を勉強しましょう。※下記も参考になります。 底面積の求め方は?高さ 底辺 上底 高さ 台形 De senaste tweetarna från @ebiebi__1373 三角形の面積は 底辺×高さ÷2 で求める。 それだけをポンと渡されてなぜそうなるのかを知らないから、全然覚えられないし、応用ができなくてとても困っていました。 最近読んだ本でそのなぜを知ることになり衝撃を受けたのですが
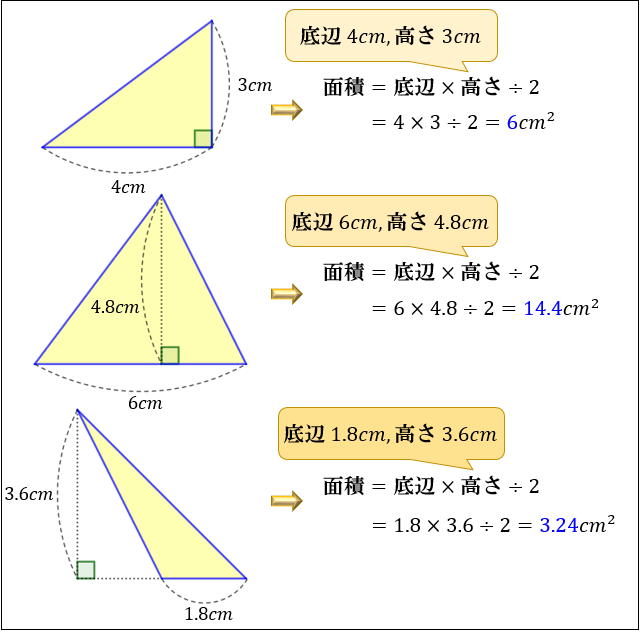
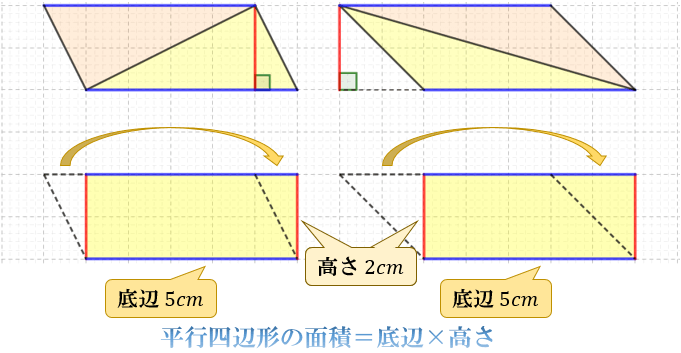
底辺×高さ÷2=三角形の面積 8㎠ くふう! 長方形に形を変えて求めた。 底辺 5cm 高さ 4cm 平行 へいこう 四辺形 し へんけい の面積 底辺 ていへん ×高さ たか 底辺×高さ=平行四辺形の面積 ㎠ 名 前 三角形 さんかっけい の面積 底辺 ていへん ×高さ たか 高 ・三角形の面積は「底辺×高さ÷2」です ・図で三角形1の面積は下底5㎝×高さ4㎝÷2 ・三角形2の面積は下底7㎝×高さ4㎝÷2 (24ページより) これで24㎠という答えが求められるわけですが、「高さ÷2」という部分は共通であるため、まとめることが可能。 19三角形の面積なぜ、「底辺×高さ÷2」なのか? 円周率なぜ、「314くらい」なのか? 21円の面積なぜ、「半径×半径×円周率」なのか? 22図形の拡大図形を2倍に拡大すると、面積や体積は何倍になる? 23錐の体積なぜ、三角錐の体積は
30=(2下底)×5÷2 下底=12-2=10 です。もちろん、同じ要領で上底も計算できます(但し、下底が既知の場合)。下底を10、面積30、高さ5のとき、 30=(上底10)×5÷2 上底=12-10=2 ですね。 台形の底辺と面積の関係 台形の底辺と面積は下式の関係が 平行四辺形の面積の公式では底辺×高さ、三角形では底辺×高さ÷2なのに、なぜ長方形は、底辺や高さという言葉を使わずたて×よこなのでしょうか。また、なぜたてが初めにきて横ではないのでしょうか。 数学 解決済 教えて!goo平行な2本の対辺を台形の底辺 と 用語で表現するなら(上底 下底)×(高さ)÷ 2 である。この公式は、台形を対角線で2つに分けたときの各々の三角形の面積が ah/2 および bh/2 であることから得ら



なぜ三角形は底辺 高さ 2なのですか どうして 2がはいるのです Yahoo 知恵袋




が分かりません Adm解き方 Dbmの比が4 3になるのは分かるのですが なぜ二 Clear
第1回 ガウス・ボンネの定理から底辺×高さ÷2の公式へ 本書 (ピタゴラスの定理でわかる相対性理論) p 6566では, 球面三角形の面積について解説を行ったのですが, じつは紹介仕切れなかったことでとても面白い話があり, 今月はその話をしてみたいと アタリマエ! |当たり前だけどアタリマエじゃない事を、アタリマエにする 統計学 エビデンスとは何か。 証拠・根拠との意味合いの違いについて 19年1月12日 Tooda Yuuto アタリマエ! エビデンスとは、「証拠・根拠」を意味する英単語「Evidence」にS:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校
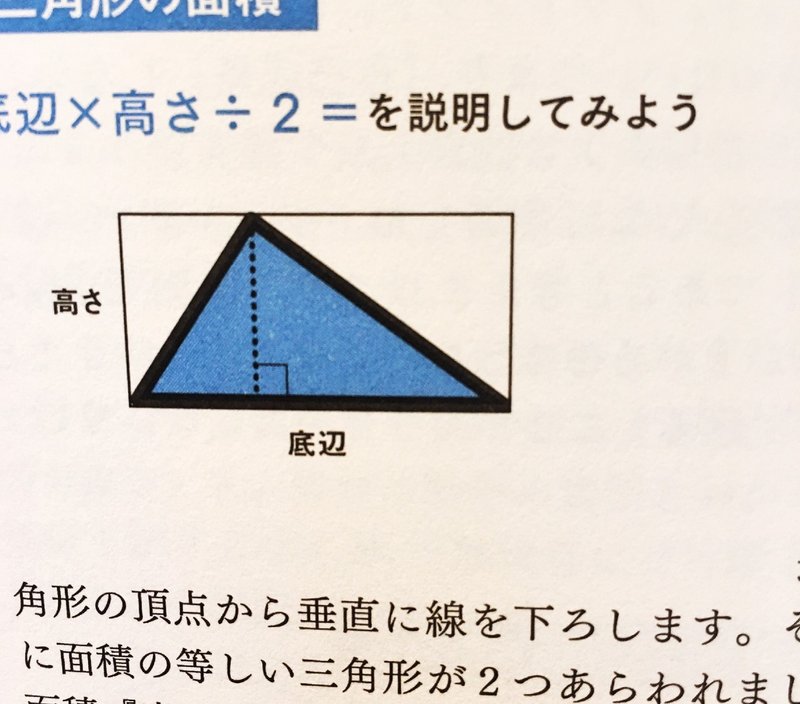
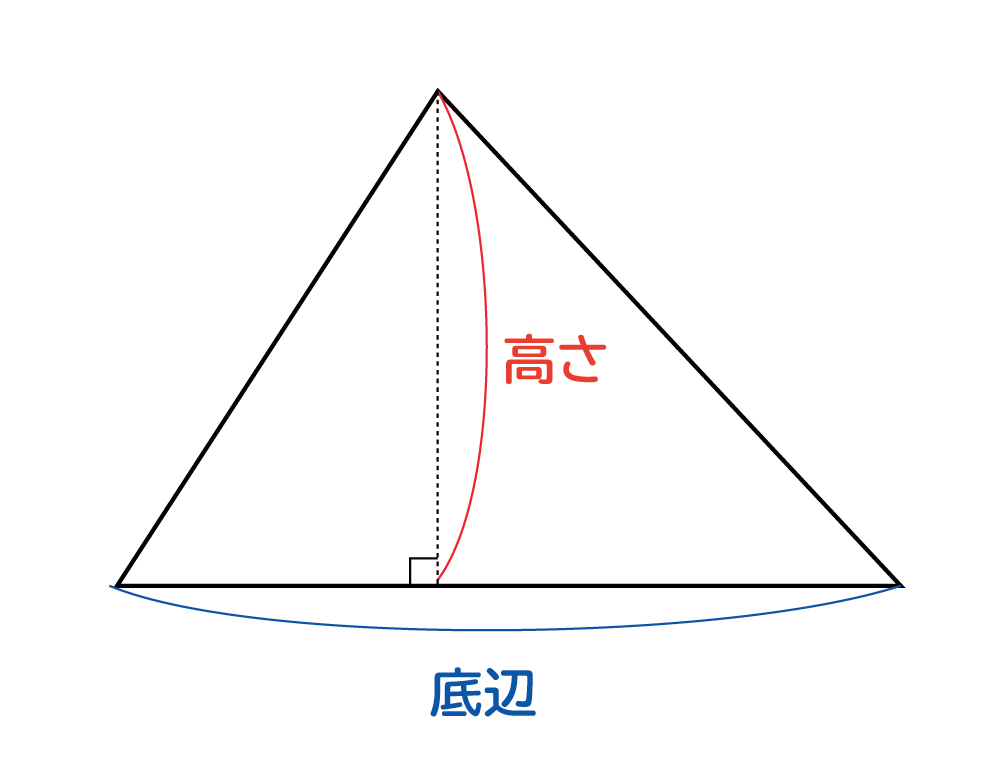
はなく、なぜ、底辺×高さ÷2で、三角形の面積が求められるのかを学習 します。底辺×高さは、四角形の面積になるので、それを半分にすること で三角形の面積が求められるという「÷2」という考え方を図や計算式を 使って学びます。 なぜ(底辺)×(高さ)÷2なのか ここで重要となってくるのが "平行四辺形の面積" です。 平行四辺形の面積は、上の図のように 切り貼りすることで長方形の面積と等しくなります。 底辺×高さ÷2で①の面積を求めることができます。 鋭角三角形 下図の様に補助線を引きます。 鋭角三角形は直角三角形が二つあると考えると分かりやいです。 鈍角三角形 このような鈍角三角形の面積は「底辺×高さ÷2」で説明できるのでしょうか。三角形の面積は、「底辺×高さ÷2」である



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
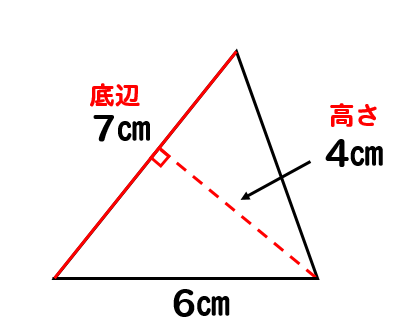
に分ける。三角形ABFの面積を,底辺をAB, 高さをFHとして求めると, 6×8÷2=24(c㎡) となる。 三角形BEFの面積を,底辺をBE,高さを CFとして求めると, 3×4÷2=6(c㎡) となる。 したがって,四角形ABEFの面積は, 246=30 で,30c㎡である。三角形の面積の求め方の基本は、「底辺×高さ÷2」です。 三角形abcにおいて、簡単のため最も長い辺をbcとします。 頂点aから辺bcに下した垂線の足をhとすると、 直角三角形abhにおいて、三平方の定理からah^2=ab^2 三角形の面積はなぜ底辺×高さ÷2なの? 先生「四角形は三角形2つなので四角形の面積を求めて2で割ればいいから、底辺×高さ÷2で導けます」 人間達「はーい!」 イッチ「なんでや」 先生「では次の問題へ進みます」 人間達「はーい!」 ワイ「なんで2で割るんや」 先生「ぺちゃくちゃ」



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




直感的に求めよう 直角三角形の面積の求め方 パパが教える算数教室
それぞれの三角形の面積は、底辺×高さ÷2より、 ( oabの面積)=oa×bh÷2 ( ocaの面積)=oa×ck÷2 したがって、 oab oca = (oa×bh÷2) (oa×ck÷2) = bh ck となります。 まとめると、 oabと ocaは底辺が共にoaで共通であることから、その面積の比は高さの比になります。 円錐・角錐の体積は「底面積×高さ÷3」になるのはなぜ? 三角形の面積の公式は、「底辺×高さ÷2」です。 「なんで2で割るの?」と聞かれたら、答えは簡単。 「この三角形と同じ三角形を上下ひっくり返してくっつけてごらん。 平行四辺形になったでしょ。 底辺×高さ÷2ってのは 三角形の面積の式ですから直角三角形にこだわる必要はありませんよ 対角線を一本引いてみてください すると底辺をa、高さhの三角形と、底辺をb、高さhの三角形の二つに切ることができるでしょ 底辺aの三角形の面積はah/2 底辺bの三角形の面積はbh/2 二つの



今週の1題




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
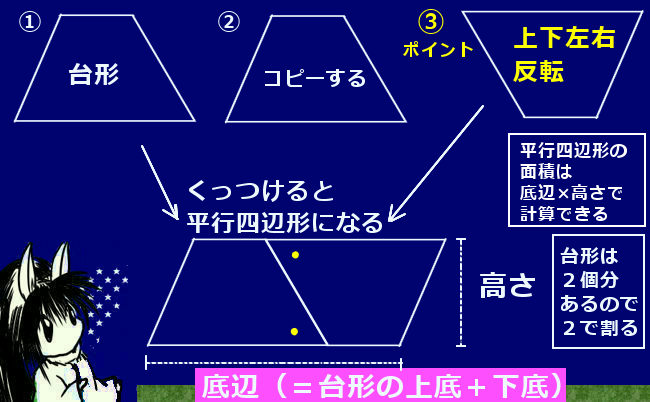
中学校2年平行四辺形9/10時間・三角形と四角形17/19時間(東京書籍:新しい数学2 p141) 思考の開始 ・三角形の面積は,(底辺)×(高さ)÷2で求められ, どの三角形も底辺BCが等しく高さも等しいから。 ・底辺と高さが等しいから。この平行四辺形の面積は『底辺×高さ』で求めることができ、底辺は元の台形の(上底下底)にあたります。 そして平行四辺形は 求める台形の2つ分の大きさなので、台形の面積は『(上底下底)×高さ÷2 ÷ 2 』となるのです。なぜ三角形の面積は底辺 × 高さ ÷ 2 で求められるのでしょうか? 直角三角形を考える 底辺が 6cm、高さが 4cm の直角三角形を考えてみます。 この三角形はたてが 4cm、よこが 6cm の長方形のちょうど半分です。 長方形は 4 × 6 = 24cm 2 なので、三角形は 24 ÷ 2



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




底辺 高さ 2 デザインtシャツ通販 Tシャツトリニティ
この扇形をひたすら細かく刻んだものをイメージします。 これをキレイに並べます。 これはほぼ三角形です。 三角形の面積は、そのカタチに関わらず、(底辺)×(高さ)÷2で求められますから、全てを一つの三角形にまとめたとみなして計算しても同じ結果が得られます。なぜ 、台形の面積 三角形の面積=底辺×高さ÷2 台形の面積=(上底+下底)×高さ÷2 まず、台形の面積に注目してみましょう。 台形の面積=(上底+下底)×高さ÷2 では、上底が0だとどうなります 求める鈍角三角形の面積は、図の赤い長方形の面積と等しいことが分かります。 赤い長方形の縦の長さは高さ÷2、横の長さは底辺なので、鈍角三角形の面積は底辺×高さ÷2ということが分かります。 鈍角三角形の面積はなぜ底辺×高さ÷2 part2




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
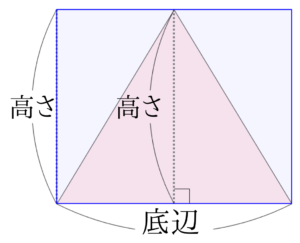
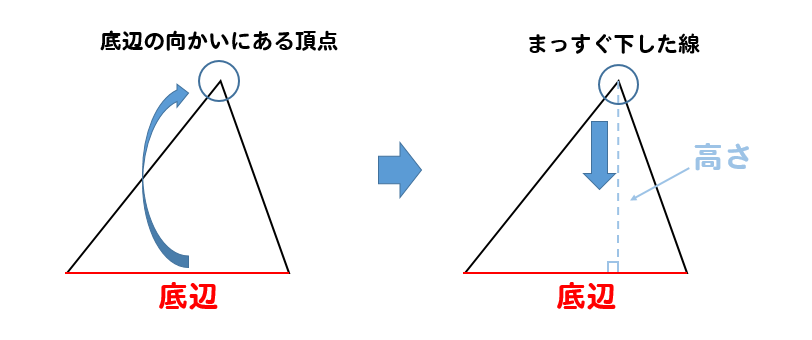
2 三角形の面積の変化をシミュレーターで実験して理解しよう! 3 三角形の面積は「底辺×高さ÷2」であり、頂点がいくら移動しても面積は変化しない! 4 次回は直角三角形の公式について確認していきます! 底辺 × 高さ ÷ 2 で計算することができます。 円の面積は「半径」の1つだけがわかれば答えが出ましたが、 三角形は「底辺」と「高さ」の2つが必要になります。 ここで必要になるのが「変数」というものです。 変数とは?? 変数とは数字の入れ物です。三角形の面積は、 (底辺) × (高さ) の 長方形 の 半分 だから (底辺) × (高さ) ÷ 2



なぜ三角形は底辺 高さ 2なのですか どうして 2がはいるのです Yahoo 知恵袋



三角比の定義は 1分でわかる定義 覚え方 表 直角三角形と単位円との関係




至急 2番の問題なのですが なぜsigna 0になるのですか Clear



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



変位を求めるとき 写真のように長方形と三角形の面積に分けて考えるのは分かる Yahoo 知恵袋




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



1



なぜ三角形の高さがb Dになったのですか また この面積比になる仕組 Yahoo 知恵袋



Q Tbn And9gct71t318twmynw63dxmqoj5dsomuiz6o0rnzjk6hursgayaq9 L Usqp Cau
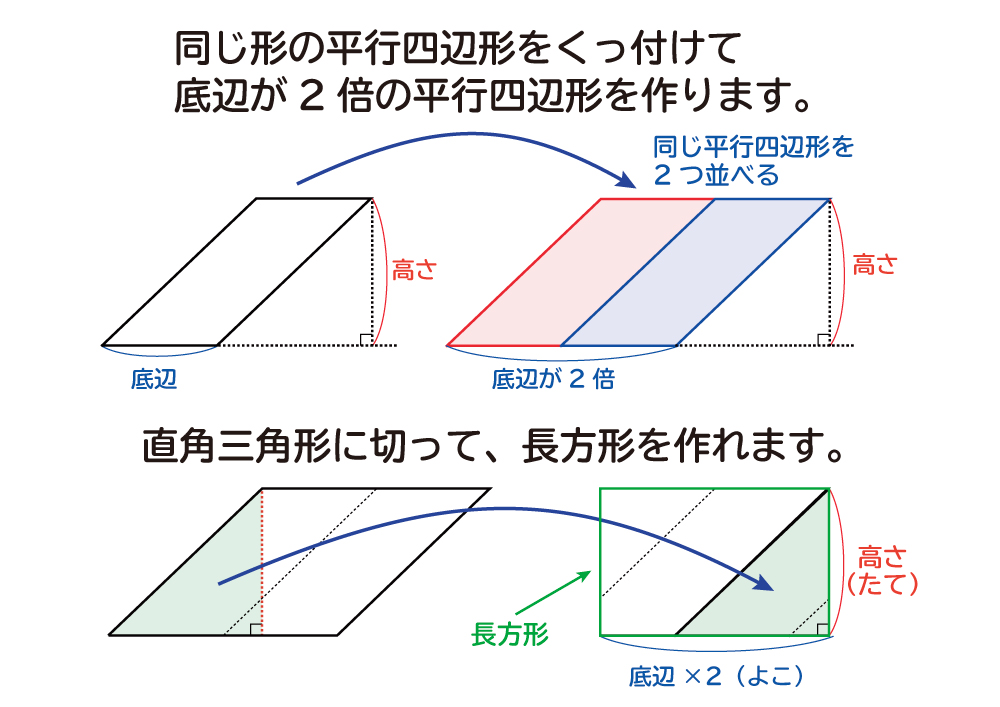



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例
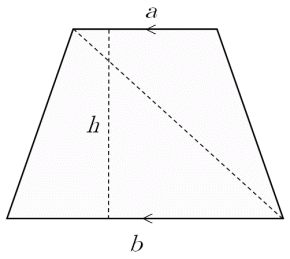



初等幾何 台形の面積はなぜ 上底 下底 高さ 2 なのか 大人が学び直す数学
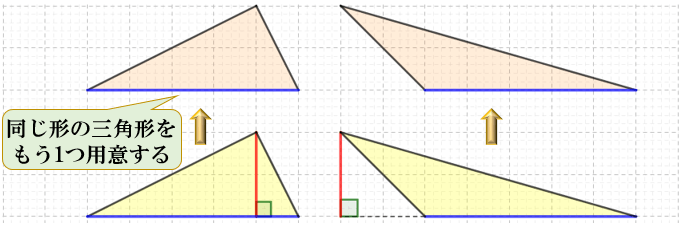



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
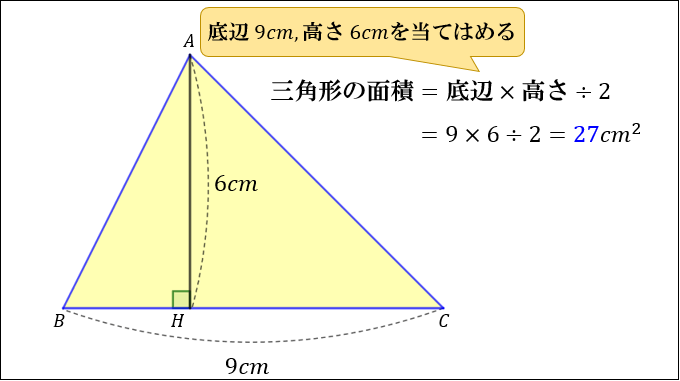



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



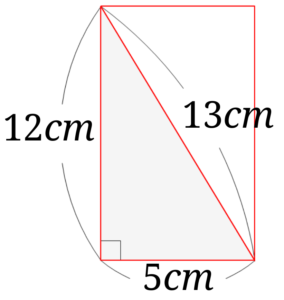
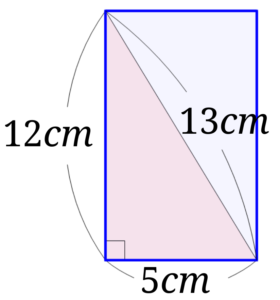
斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




なぜ底辺と高さが同じなら全ての三角形の面積は等しいのか 数学が嫌いなんです




三角形の面積の公式 2 って どうして2で割るの




三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



数3 図3の三角形の底辺と高さが何故 1 T 2となるのか分かりません Yahoo 知恵袋



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
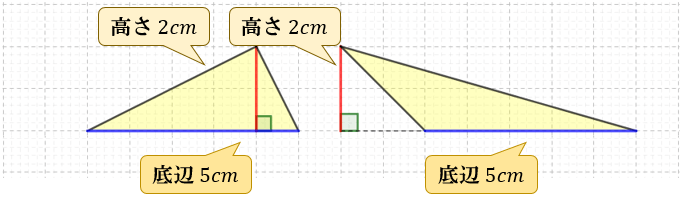



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
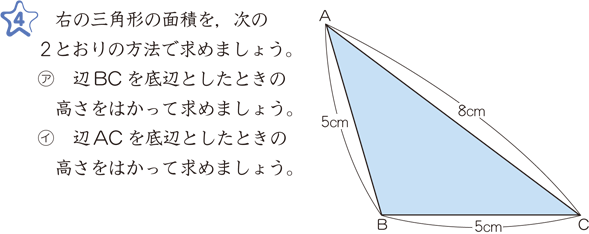



底辺と高さ 算数用語集




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
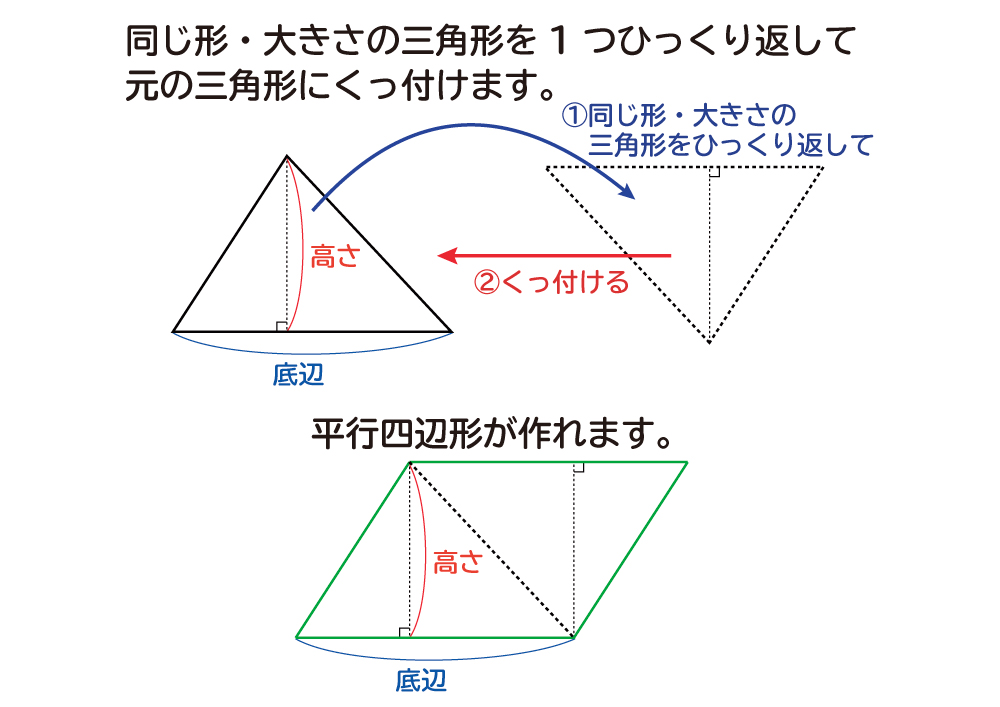



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
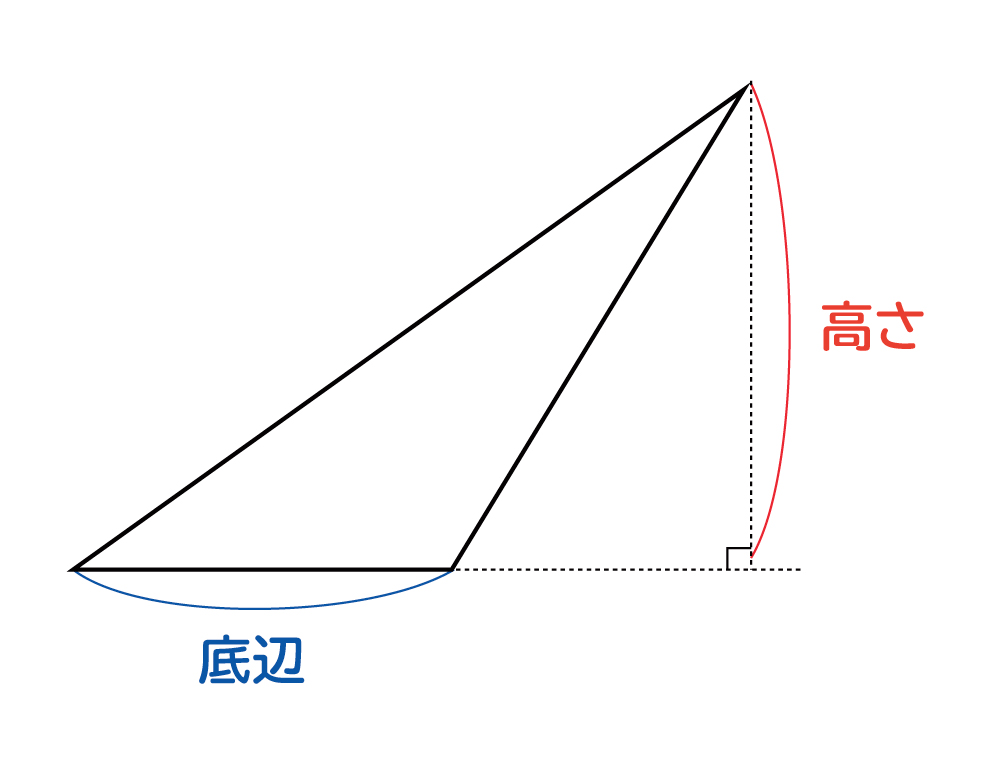



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




三角形の面積って 底辺 高さ 2 ではありませんでしたか それとも今回 数学 教えて Goo



3
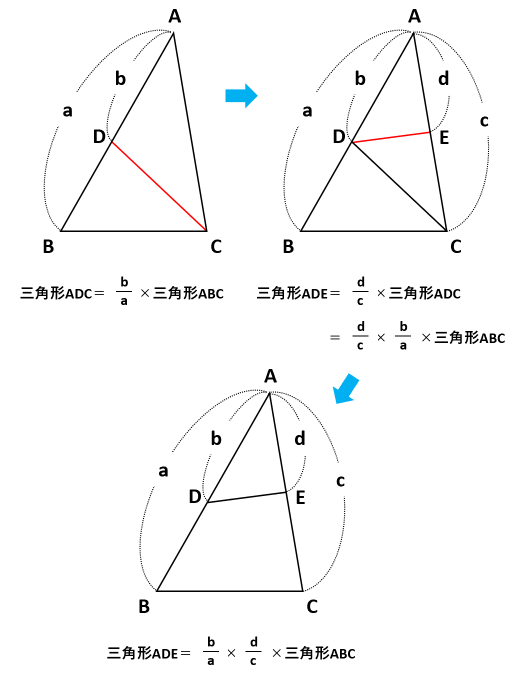



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook




底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo
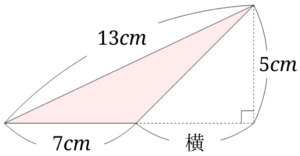



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
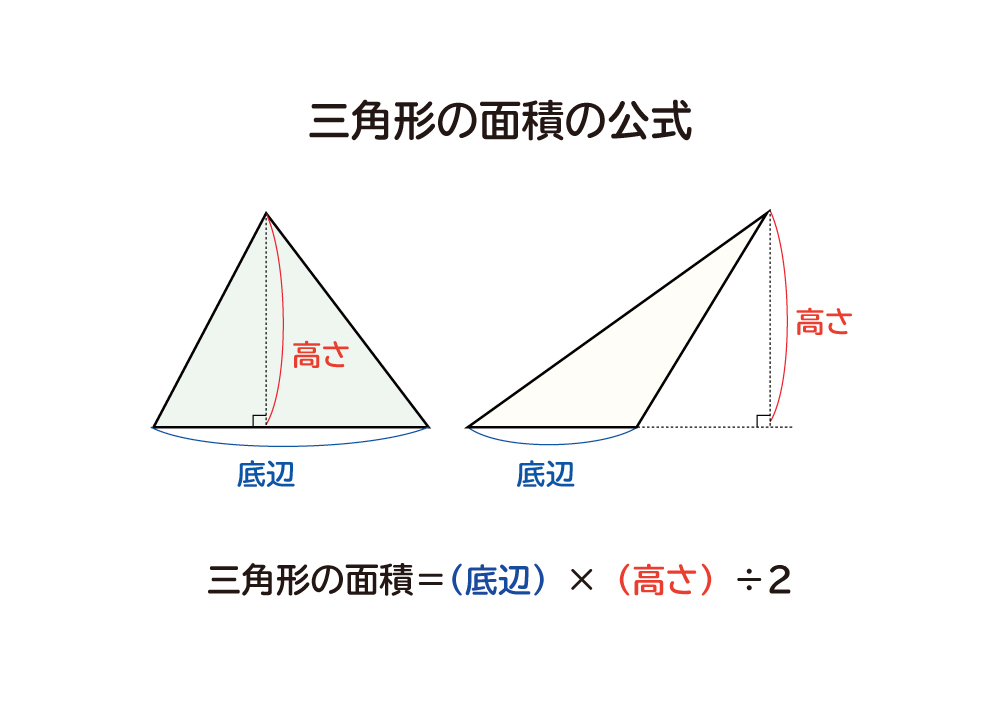



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
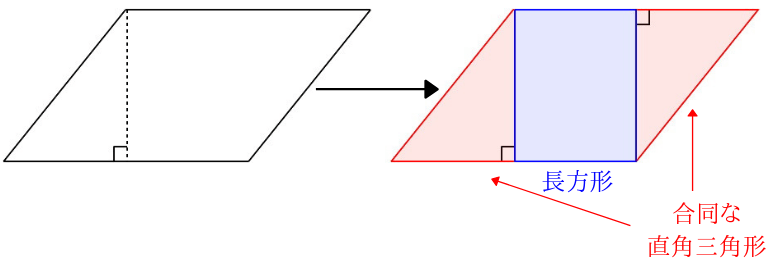



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校




三角形の面積の公式 算数の公式
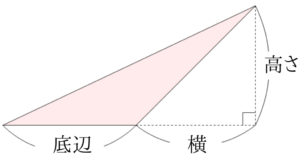



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校
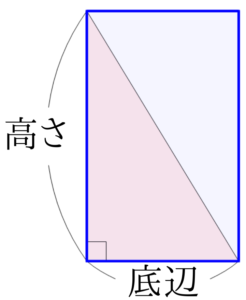



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト
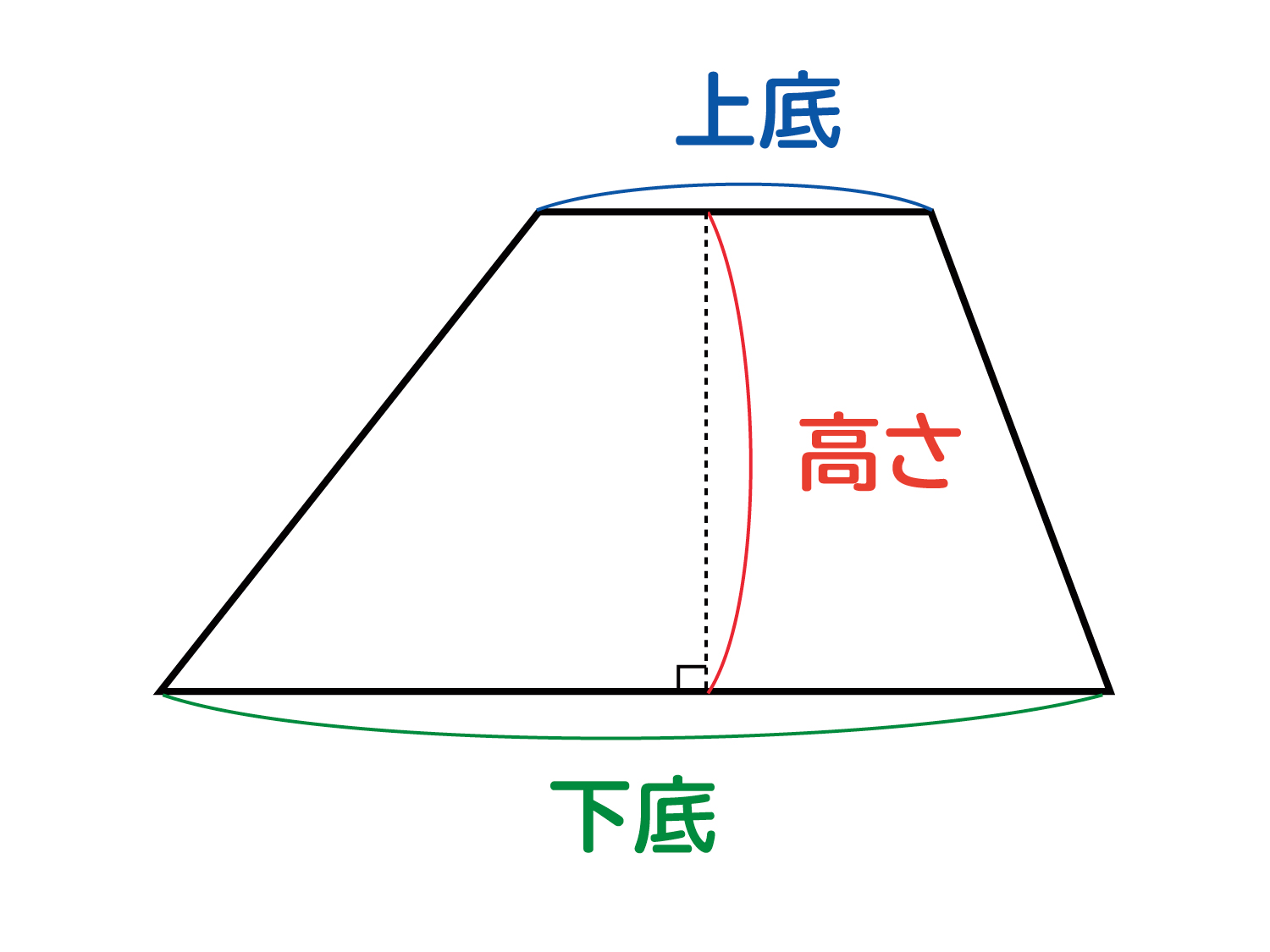



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
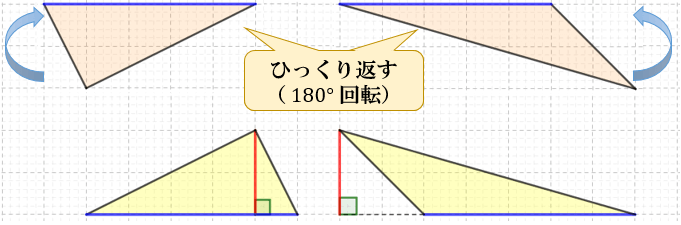



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
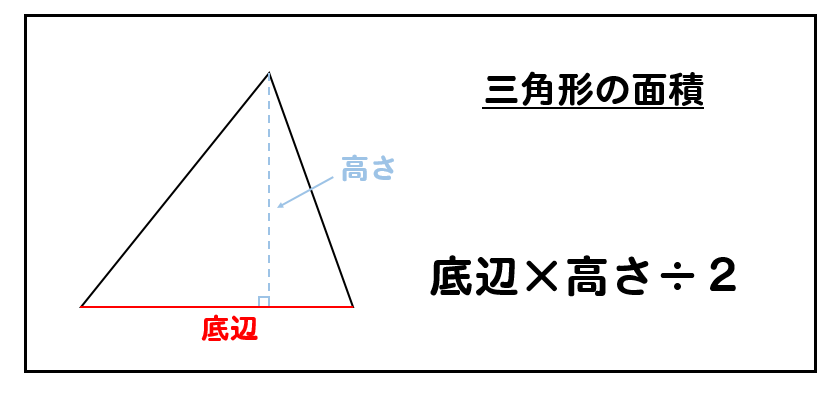



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




この問題の解説にひいてある青線のところがなぜそうなるのかわかりません Clear



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




平行四辺形の面積の求め方 公式と計算例




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




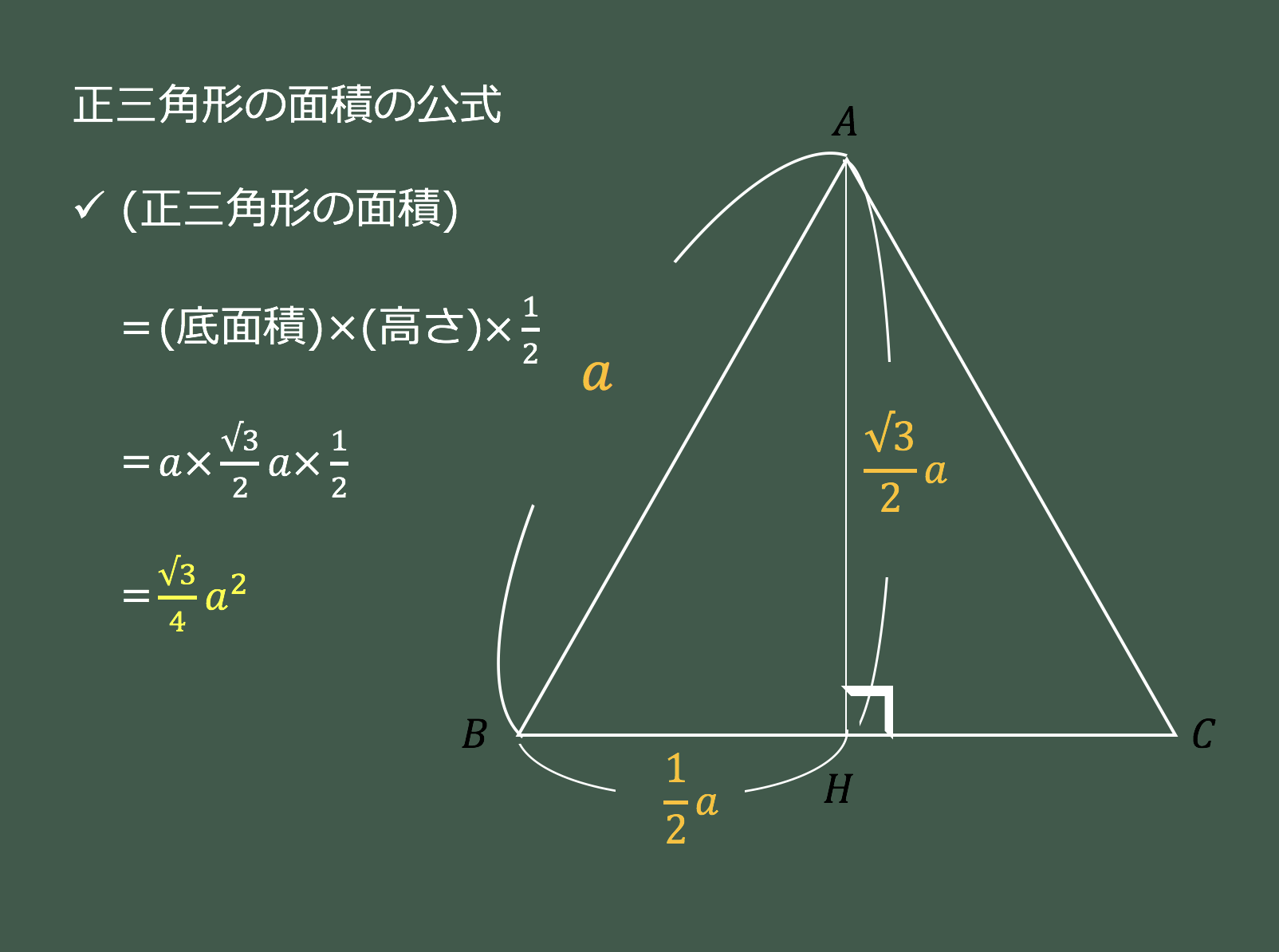
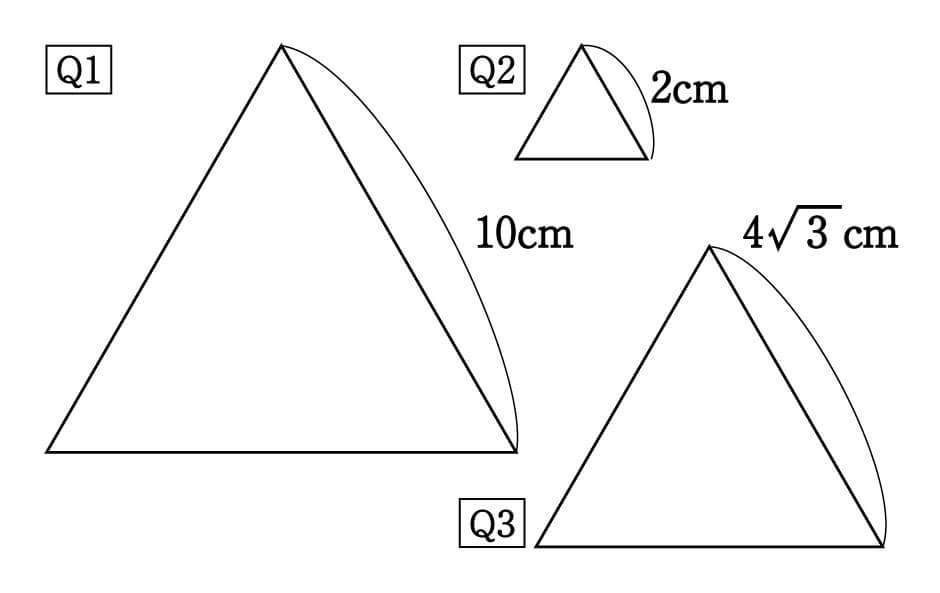
数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
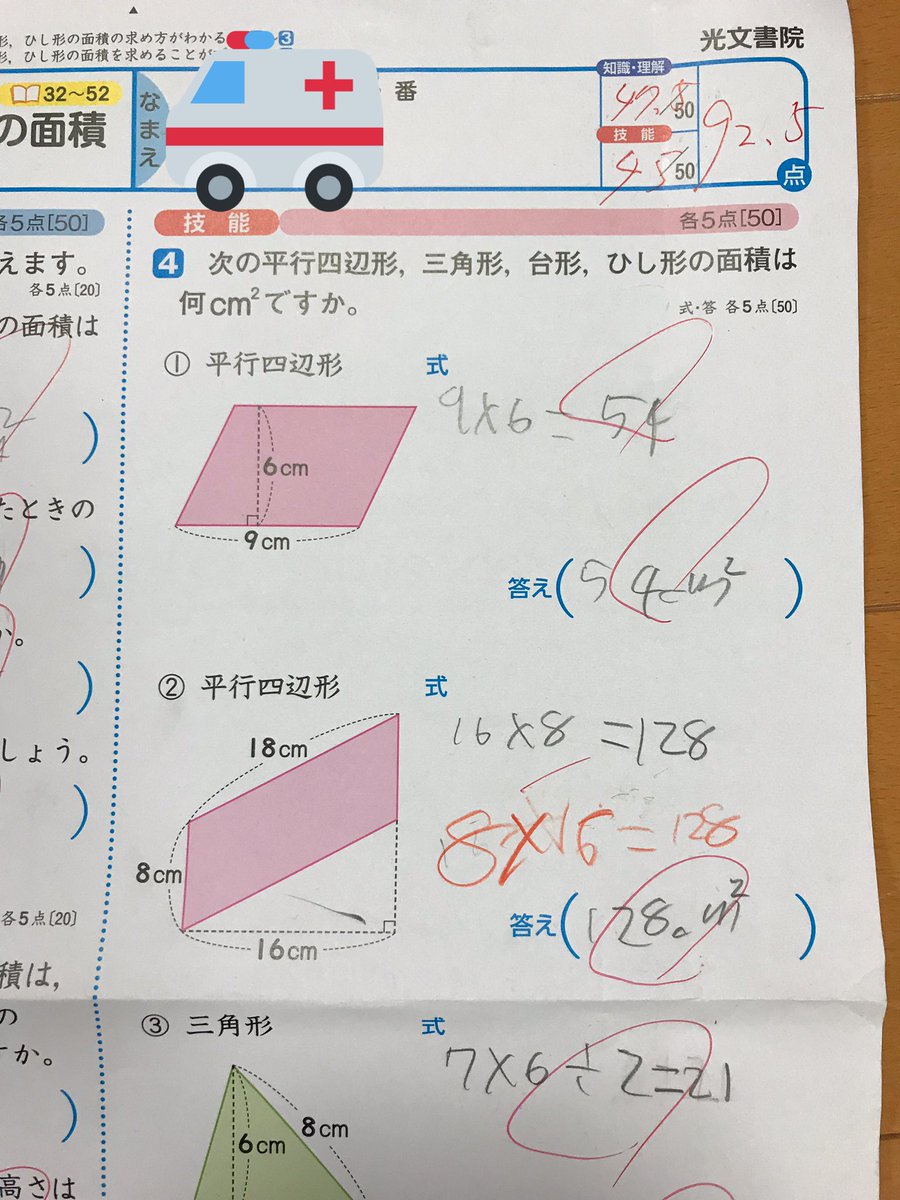



ストさん 5年生の息子の算数のテスト 平行四辺形の面積の公式は底辺 高さであり 高さ 底辺ではないから 答えは正解だけど 式は不正解でマイナス5点だと 小学校の先生は馬鹿なのか 信じられない



底辺と高さの等しい三角形の面積が等しいのはなぜですか 同じ三 Yahoo 知恵袋
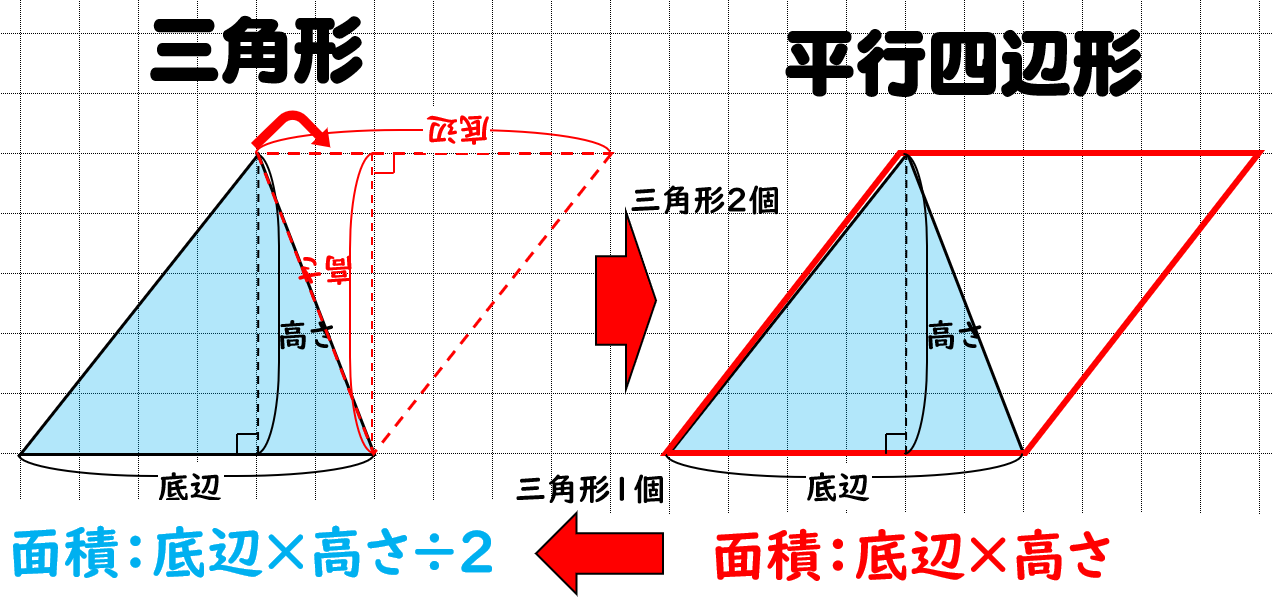



三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



1 2 ルート3
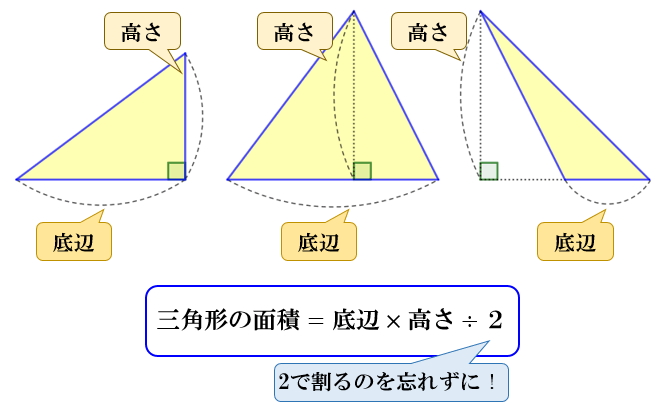



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
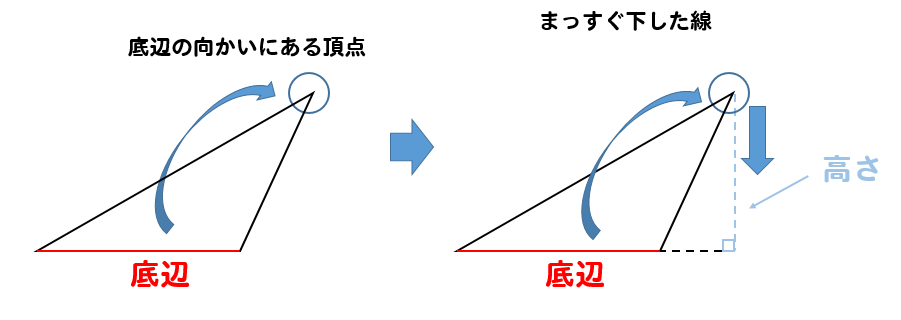



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




予習 なぜ底辺 高さ 2 三角形の面積 逆算も Youtube



1



底辺 高さ 2 のストーリー Chie Oikawa コーチ バリスタ 調理師 Note




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める




面積の求め方 計算公式一覧




平行四辺形の面積の求め方 公式と計算例



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル




三角形の面積の公式はどうして底辺 高さ 2なのか Irohabook




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学




3番の解説の黒下線部なぜそのようになるのですか Clear




わかる方教えてください 2 で なぜ底辺が Clear
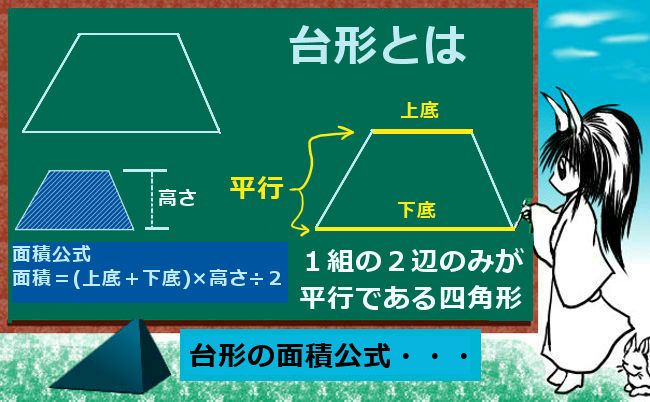



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori




なぜsinなのですか Clear
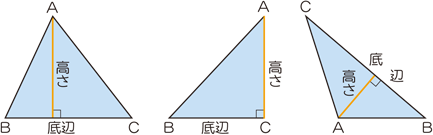



底辺と高さ 算数用語集
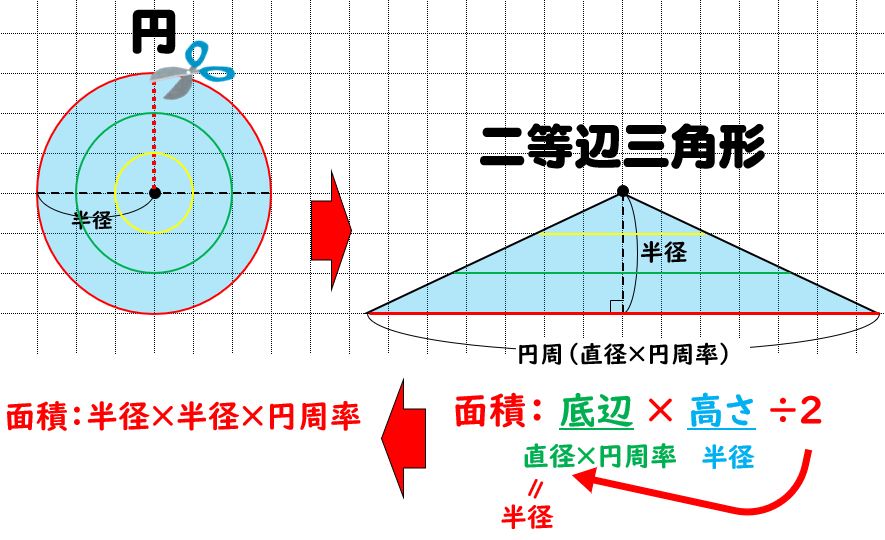



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




三角形の高さの求め方 底辺の位置によって 高さは変わる 中学や高校の数学の計算問題



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



Tan45度の値は 1分でわかる意味 値 Cos45度 Sin45度との関係



0 件のコメント:
コメントを投稿