体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。2章 空間図形 48 140 次の図の立体の体積を求めよ。 ⑴ ⑵ 138 次の図の角錐の体積を 求 めよ 。 ⑴ ⑵ ⑶ 141 右の図のよ う に ,1 辺 12 cm の立方体から,3 点 A ,C ,F を通る平 面で切ってできる 2 つの立体のうち,小さい方の立体を取り除いた。 中学数学「空間図形」③ 体積の問題のコツ 中1数学「空間図形」の3回目です。 今回は 体積の問題 で中学生がつまずきやすいところを解説します。 柱・錐・球それぞれ、入試問題中心に計6例題。 ぜんぶ応用問題ですので、基本を学んだうえで「でも
わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋
立体の体積の求め方 台形
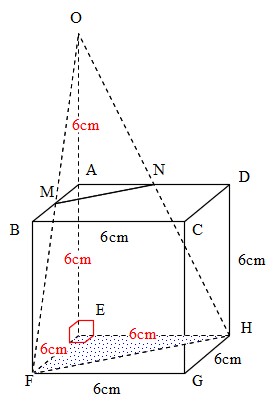
立体の体積の求め方 台形-台形の面積の求め方 (上底+下底)×高さ÷2 なので 角柱;四角錐の体積は・・・18×10÷3=60 向こう側は台形abqpを底面とする四角錐になる。 台形abqpの面積は・・・(15)×10÷2=30 四角錐の体積は・・・30×4÷3=40 よって上側の立体の体積は6040=100 全体から引くと下側も体積が出せる。 =140



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
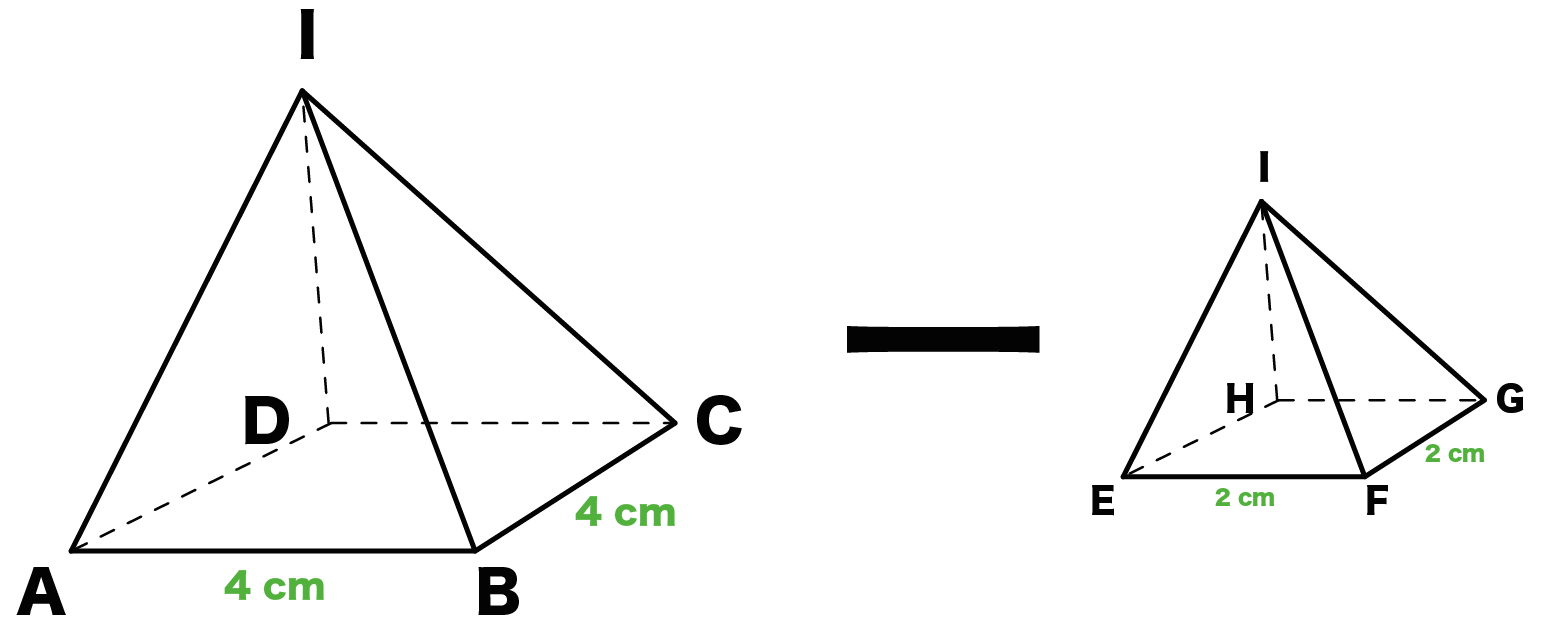
定積分で体積を求める ある曲線下の面積を定積分で求められたように、ある平面を積み重ねてできる立体の体積も、定積分で求められます。 このとき、平面の積み重ね方には大きく分けて次の \(2\) 通りがあります。 三平方の定理、立体の体積・表面積 解説 右図のような立体の体積・表面積は,四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形,側面が1辺の長さ4cmの正三角形です。四角錐や五角錐の体積の求め方 忘れている人が割といるので確認して粘土でできた立体の体積の求め方をいろいろ考え出そう。 つぶして直方体(立 方体)にする。 1ℓますに詰めて縦・ 横・高さを調べる。 直方体と捉 えて縦横・高 さを概測し て計算する。 1㎤の何個分 か調べる。 1㎤と全体 の重さから 計算する。 水に沈めて
ここで定める"等積中心線"とは,台形内の底辺と平行な直線であって, それを中心として,台形面を面と垂直な方向に移動したときにできる上下のくさび形の立体の体積が等しくなる直線である (付図 3) . 台形の下底の長さを a ,上底の長さを b ,高立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答 で、この爪形の体積を計算してみたところ、なんと 2 だったと。 ちなみに求め方は高校3年生が学ぶ「積分」というもので求め、この数値は間違いがないはずです(別々の4通りの方法で求めて全て一致したので)。 求め方そのものはここでは割愛します。
円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。台形の面積を求める公式 台形の面積を求めるときには、次の公式を使います。 下記も参考になります。 問題2- 4 次の立体の表面積と体積を求めなさい。 やり方を2通り示したいと思います。四角錐台の体積 110 /191件 表示件数 5 10 30 50 100 0 1 10 女 / 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 建築設計の折り上げ天井の空調気積と平均天井高さ ご意見・ご感想 計算式も提示頂いてるので、根拠を示せるので助かり



Mathematics 錐体の一部の体積 働きアリ




立派な 台形 体積 求め 方
円と球コンパスの使い方 がい数四捨五入する位 角180°より大きな角 面積長さの求め方 面積台形の面積 体積容積の求め方 体積複雑な形の立体 分数帯分数のひき算 倍数と約数倍数と約数の文章題台形の面積= (上底+下底)×高さ÷2 角柱の高さ (真横からみた図) (立体の向きを変えると) 角柱の体積は,底面積と高さがわかれば 公式を使って求めることができるんだね。 24 正答例と解説 6年「角柱と円柱の体積」 〔考え方の 錐の体積の公式の求め方 台形の体積の公式の求め方を知りたい!? こんにちは!この記事をかいているKenだよ。着る毛布ほしいね。 台形の体積の求め方 を教えてほしい。 そう、きかれることが結構ある。 正直ドヤ顔で、 台形の体積はね・・・ って答えそうになる。 だけれども




2番の質問です なぜ この式になるんですか 分かりやすくお願いします Clear
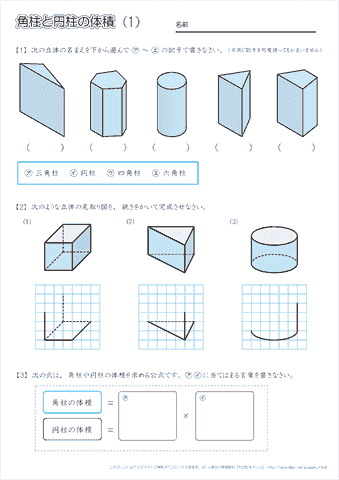



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 台形の体積の求め方 台形の体積の求め方は A A B B 2 Hで 立体の体積の求め方です 解説もお願いしたいです Clear 公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成 直方体を切ってできた立体の体積は 直方体を平面abcdで切ってで 台形の回転体 中学から数学だいすき 台形の体積の求め方 台形の体積の求め方は A A B B 2 Hで また来てね問題集 図形問題 解答と解説 中学受験 家庭教師 東京 台形の体積 って何 相似の考え方




立派な 台形 体積 求め 方
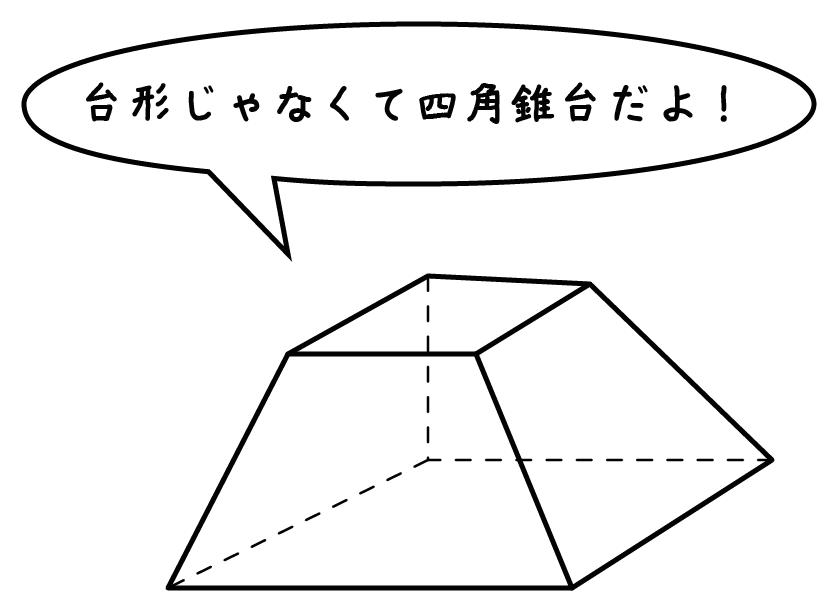



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
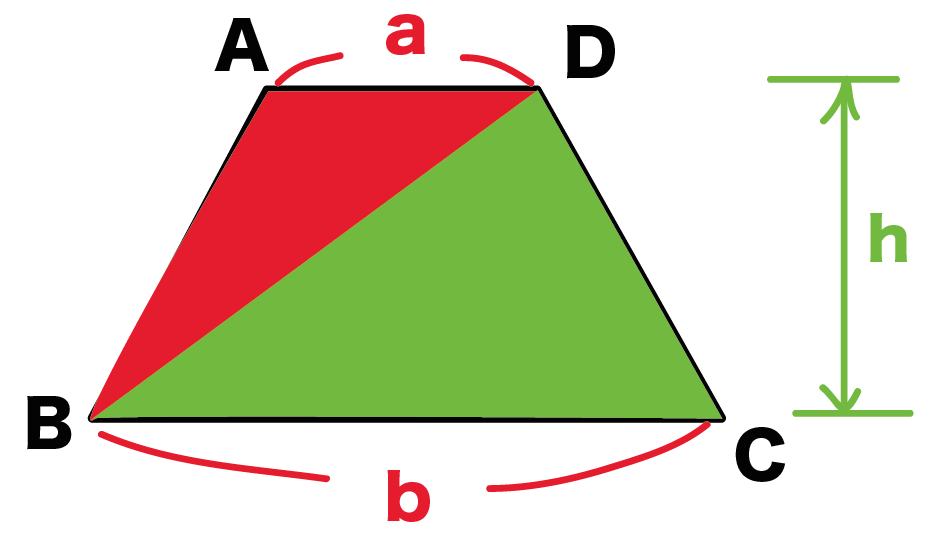
《立体の体積の求め方》 求める立体は①と②があわさって出来た立体であることから、①の直方体の体積+②の立方体の体積で求めることが出来ます。 ①の直方体の体積=8×8×4=256(cm³) ②の立方体の体積=4×4×4=64(cm³)立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cmまずは底面積を求めましょう。 ここで底面である四角形の面積を求めることになるので、ちょっと公式を確認 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式! ? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。




立派な 台形 体積 求め 方



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積
体積の計算式 (半径)2×314× 1 3 形 状 三 角 形 平行四辺形 台 形 半円筒形 立 方 体 円 錐 四 角 錐 平面形 3中線の交点又は中央の底辺から1/3の高さ 対角線の交点 台形を2つの三角形に分け、その重心を 算数これの体積の求め方教えてください まず 上の台形の面積を 四角錐台の体積 高精度計算サイト 中学受験算数 台形の面積公式は忘れても大丈夫 自分で作ろう 台形の体積 って何 相似の考え方を利用して四角錐台の体積を求め 公式の証明 体積測定にV = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積




21番は高さの求め方 22番は母線の求め方を教えてほしいです Clear
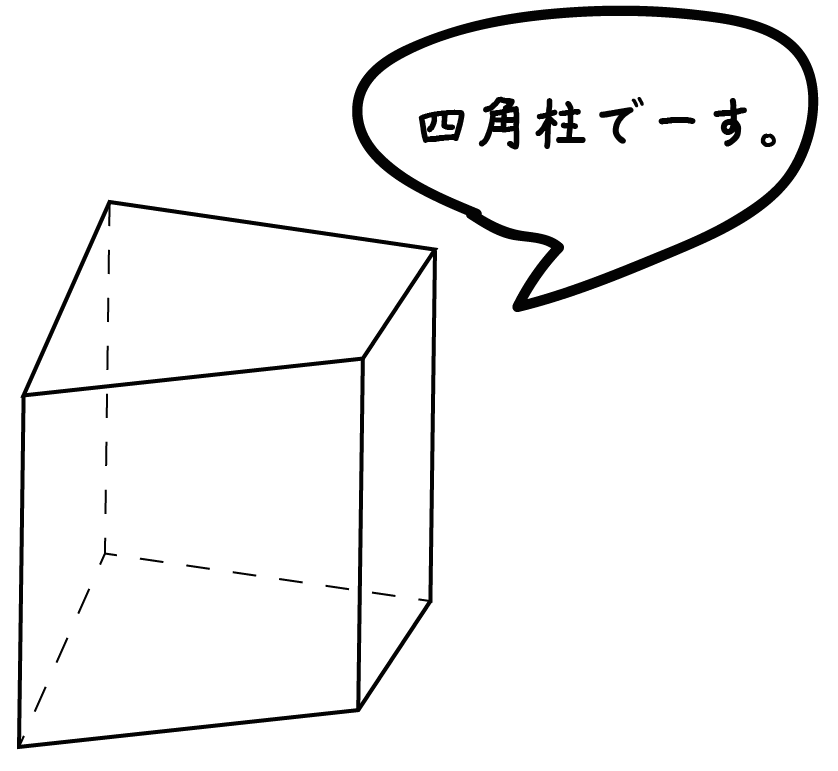



計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
この立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は,比例(相似)の関係を使って求めることができる.縦:横 x 5x=106立方体の公式と計算(求め方) 立方体の公式を下記に示します。 立方体の体積=a 3 aは1辺の長さです。その他の立体図形の体積の算定は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積1. アの体積は128cm 3 、イの体積は2512cm 3 です。 それぞれの立体の の値を求めなさい。




立派な 台形 体積 求め 方
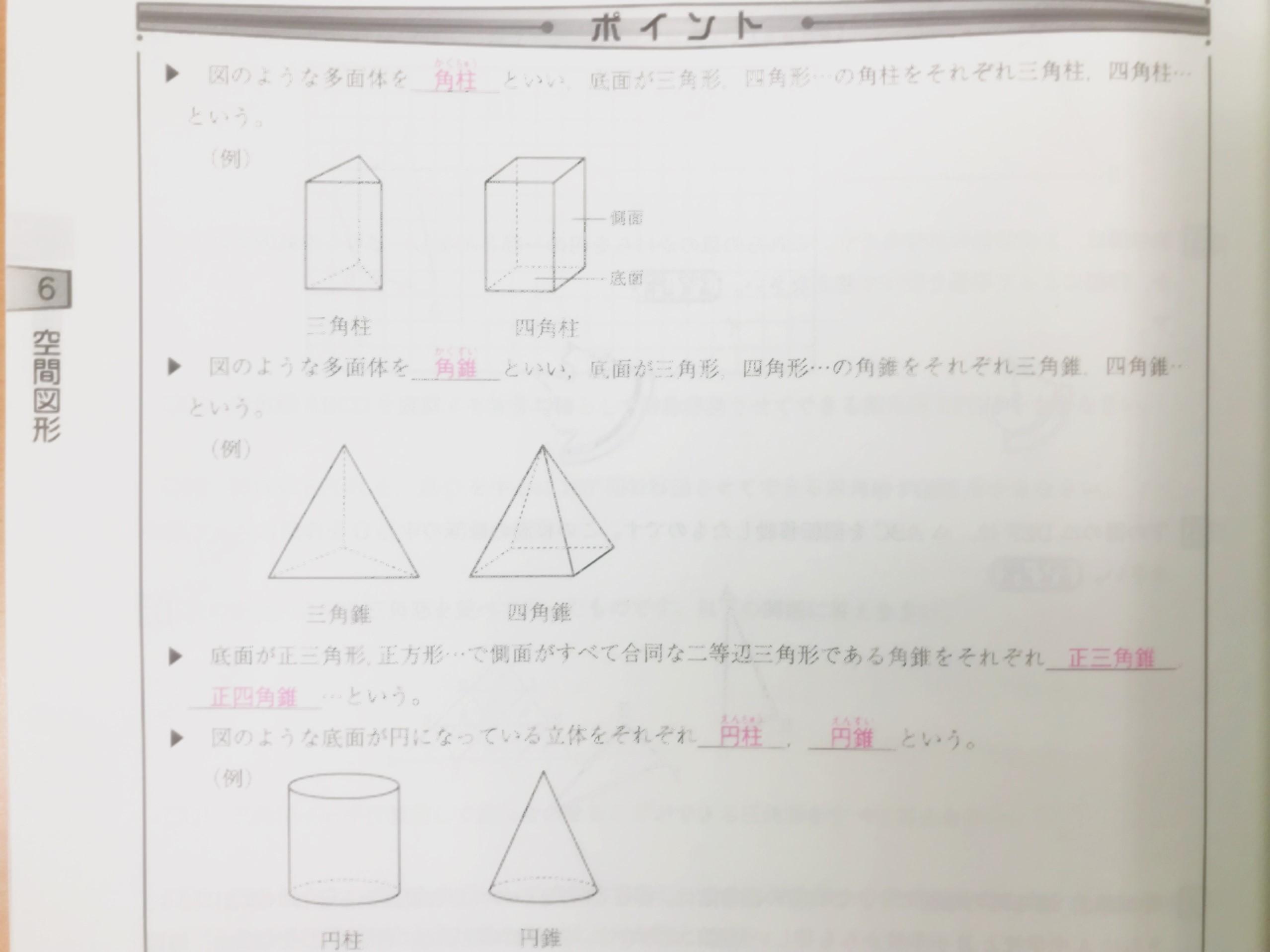



角柱 円柱 角錐 円錐の体積 滋賀県栗東市の個別塾 学習塾 ナビ個別指導学院 栗東校ブログ
錐台(すいだい、英 Frustum )は、錐体から、頂点を共有し相似に縮小した錐体を取り除いた立体図形であり、切頭錐体ともいう。 あるいは言い換えれば、錐体面と2枚の平行な平面によって囲まれる立体図形である。 円錐からできる錐台を円錐台(切頭円錐)、角錐からできる錐台を角錐台ご意見・ご感想 V=h (S1S2√(S1×S2))/3, V:体積, h:高さ, S1:下底面積, S2:上底面積この公式で算出した数値と、少数以下が多少違いますが参考にどちらが正しいでしょうか例えば 上部から数センチ下がり時の容積を簡単に計算出来ないでしょうか?台形を回転させてできる立体の体積の求め方について教えてくださ 球 の にある部分の体積 と表面積 を求めなさい 4練習問題の答え 解答1 円柱 の にある部分の体積 と表面積 を求めなさい 練習2




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
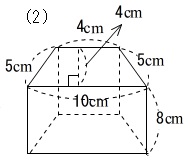



立派な 台形 体積 求め 方
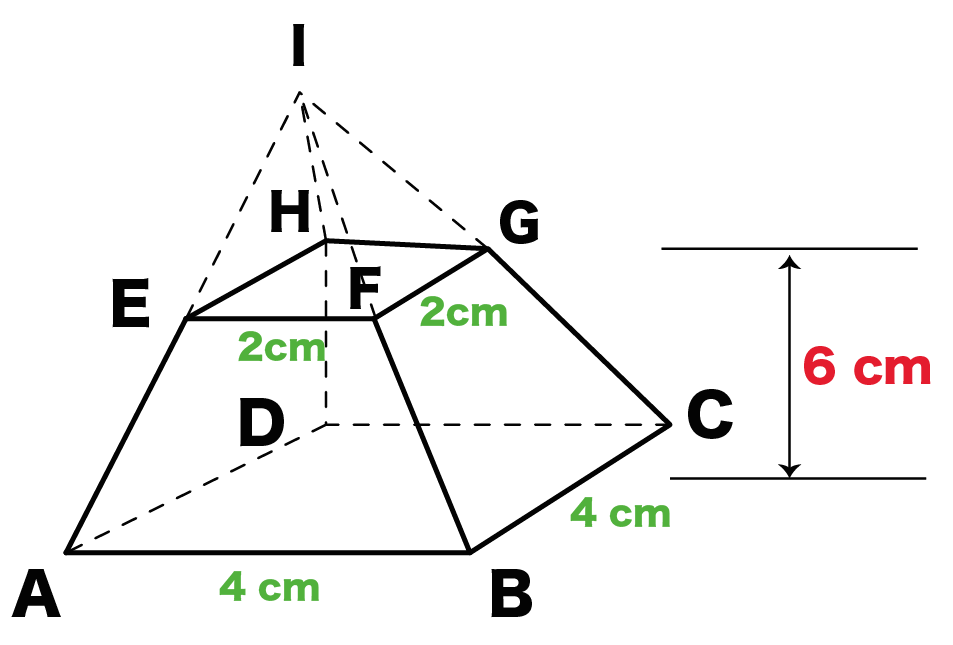
円柱 複合図形の体積の求め方 2 次の展開図を組み立てて、できあがる立体の体積を求めましょう。体積1 4解説 >> 体積1 2解説 4 次の平面図形をそれぞれ直線mを軸として1回転させてできる回転体の体積を求めよ。 6cm 3cm 10cm m ① m 6cm 8cm ② ③ m 3cm 2cm 10cm ①の台形を直線mを軸に1回転させると 図のような円柱と円錐を組み合わせた立体になる。 円柱、円錐また,それ以外の4つの面は,すべて台形で ae=bf=cg=dh=3 cmである。 このとき,次の(1)~(3)に答えなさい。 (1)(2) 略 (3) 立体 abcdefgh の体積を求めなさい。なお,途中経過の計算も書くこと。




台形の面積の求め方 公式 小学生 中学生の勉強



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋
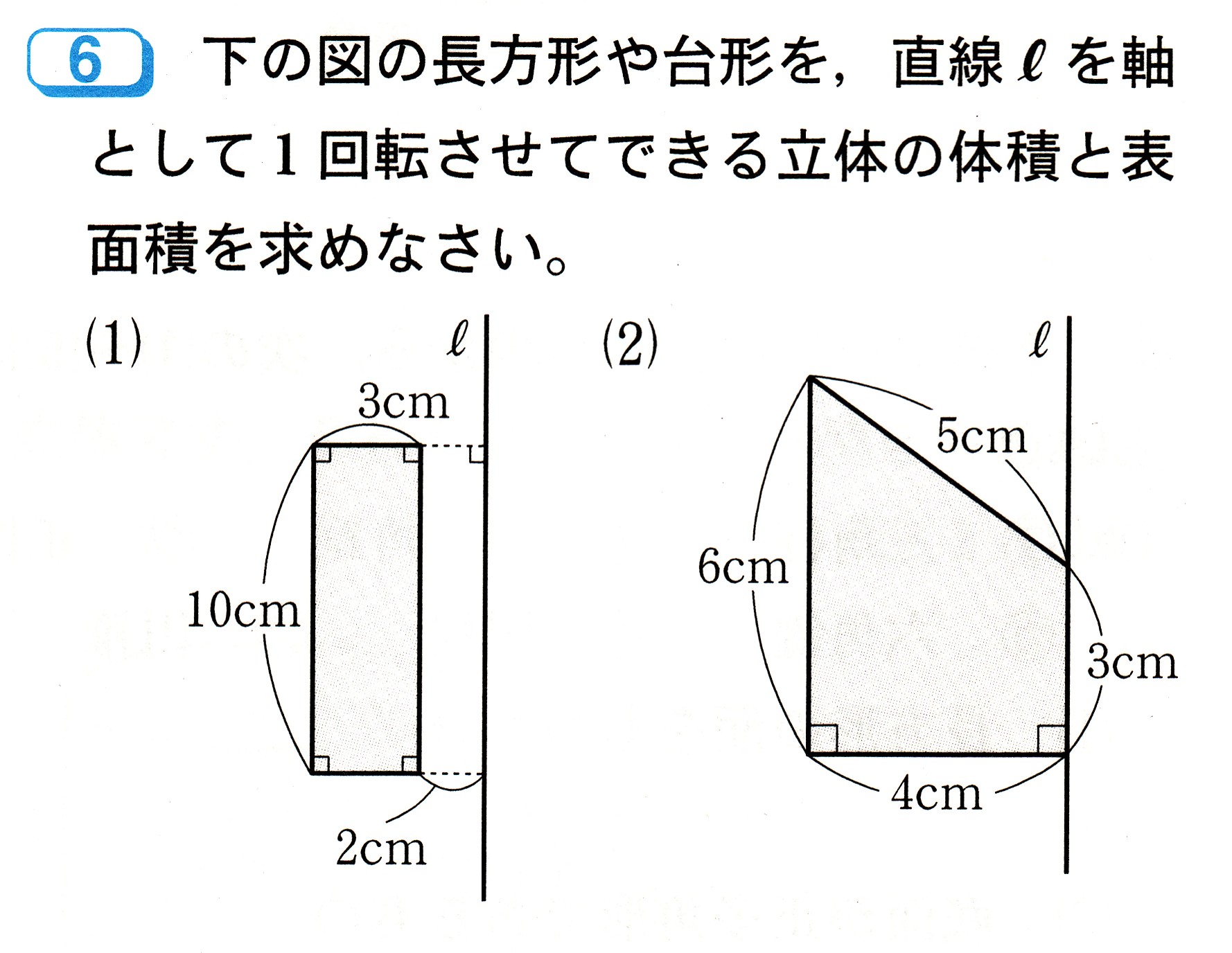



中学1年数学 立体の表面積と体積 確認問題6 あんのん塾




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



1




体積測定によって検証する土塁の取崩しと土橋の造成




台形の面積の求め方 公式 小学生 中学生の勉強




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



地図の体積計測



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



台形の体積の求め方 台形の体積の求め方は A A B B 2 H Yahoo 知恵袋



Math ややこしい立体の体積は 柱と錐に分割して求める 働きアリ



1
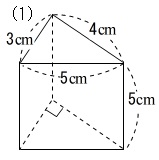



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球




Abcd Efghy 1right Righ Descubre Como Resolverlo En Qanda




空間図形14 円すい台の体積 Youtube




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




ねじれの位置の問題を解く 苦手な数学を簡単に




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




表面積の求め方 計算公式一覧
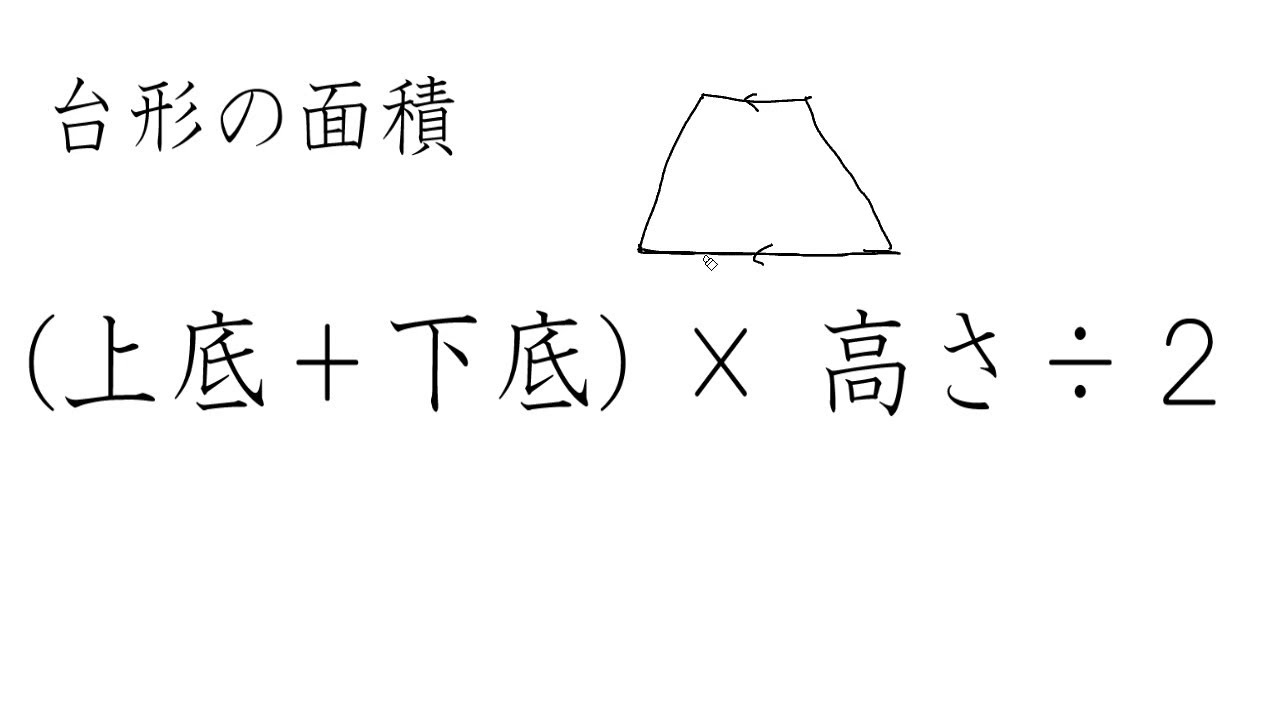



台形の面積の公式 Youtube




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋




3 4 Descubre Como Resolverlo En Qanda
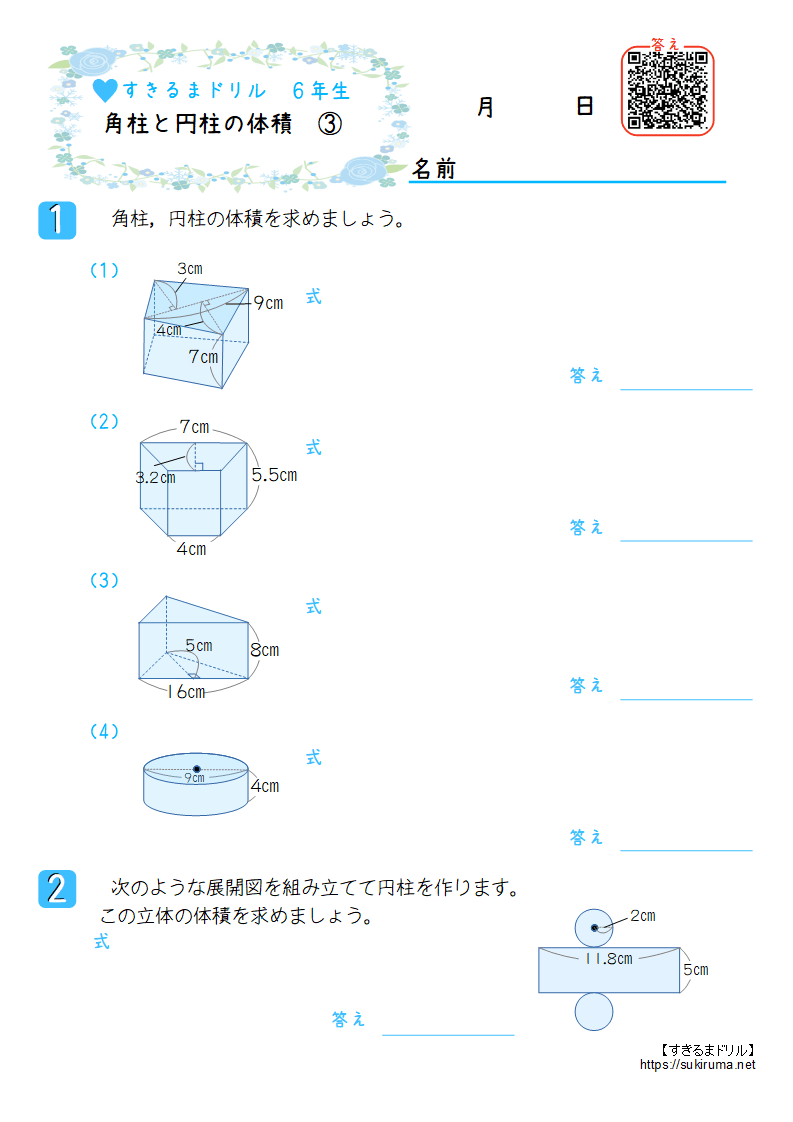



すきるまドリル 小学6年生 算数 角柱と円柱の体積 無料学習プリント すきるまドリル 無料学習プリント




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座
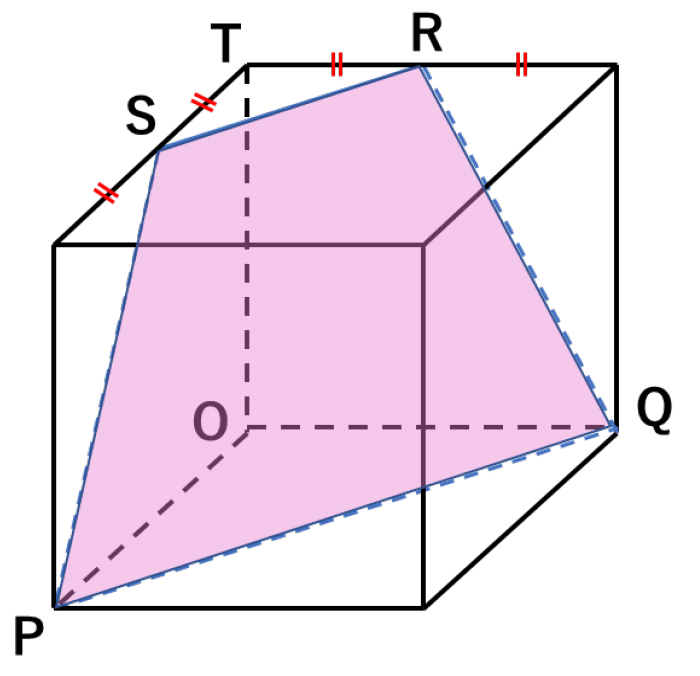



よく見かけますね この展開図 後編 中学受験プロ講師ブログ




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
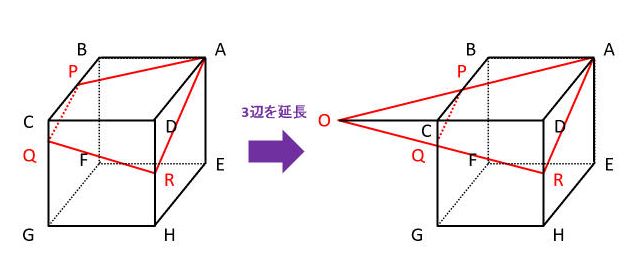



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



台形を回転させてできる立体の体積の求め方について教えてください Yahoo 知恵袋




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
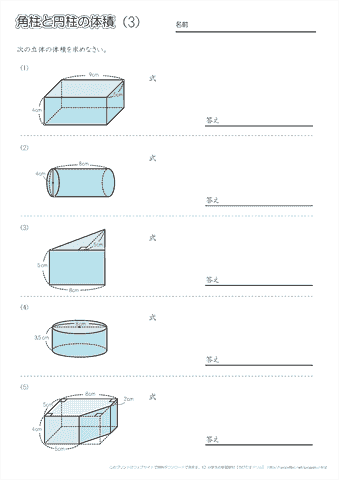



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




立派な 台形 体積 求め 方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
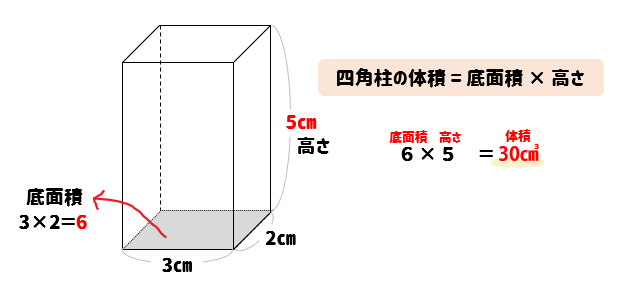



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




立派な 台形 体積 求め 方



立派な 台形 体積 求め 方



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積




立派な 台形 体積 求め 方



立体の体積 テストの前に



Q Tbn And9gct2juwikqj2sust9aqmlej1kyutmmej9agmdvdc75hiyxdbuisi Usqp Cau



この台形の回転体の体積と表面積を教えて下さい 求め方と解答を至 Yahoo 知恵袋



Xp9ax13dult21c0wtxqar30g7ld Com Oosaka Sugaku F H29 8 25 Q4



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




台形abcdを 辺abを軸として1回転させてできる立体の表面積を求めなさい Clear




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




立派な 台形 体積 求め 方
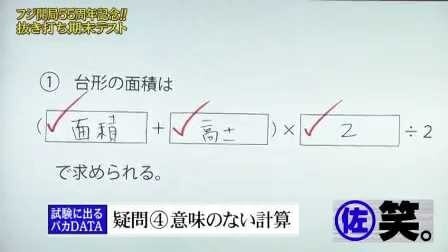



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
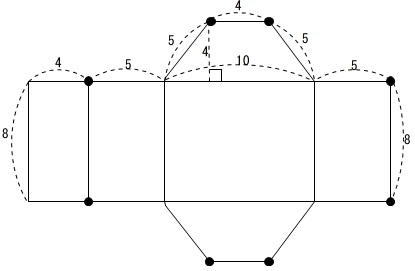



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球
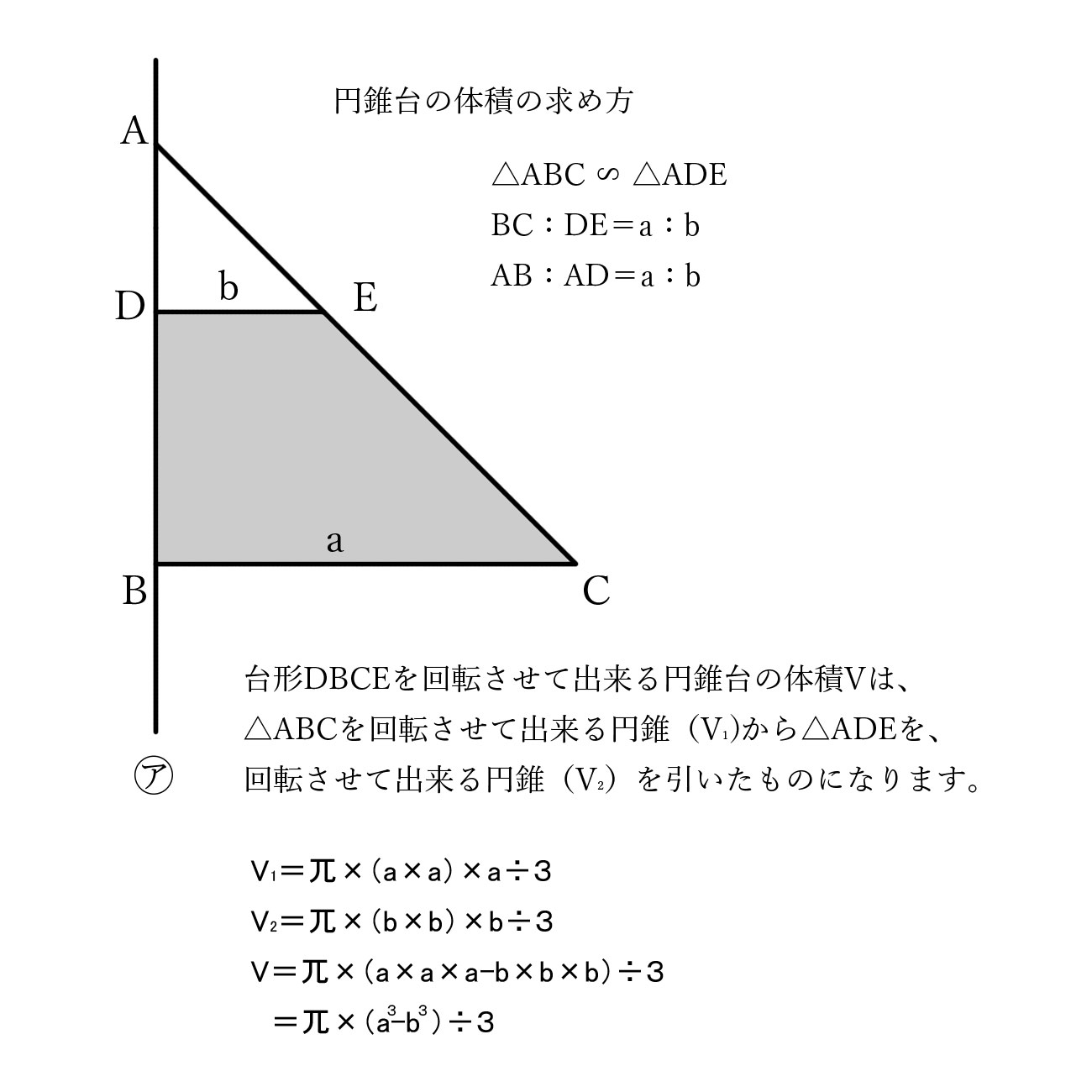



立派な 台形 体積 求め 方




四角錐台の体積 高精度計算サイト




台形の体積を求める 下図のような上底80mm 下底100mm 高さ90m Okwave



3




立派な 台形 体積 求め 方
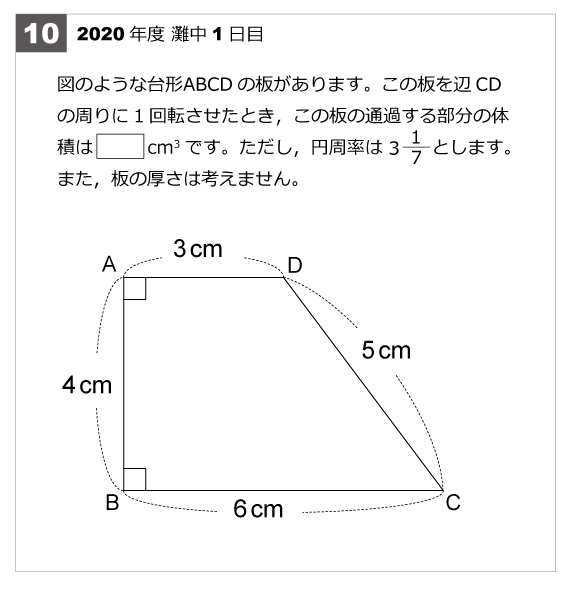



灘中解説速報 年第10問 台形の回転体 算数星人のweb問題集 中学受験算数の問題に挑戦




立派な 台形 体積 求め 方




立方体の切断の問題 16年本郷中 元オカマの家庭教師の独り言
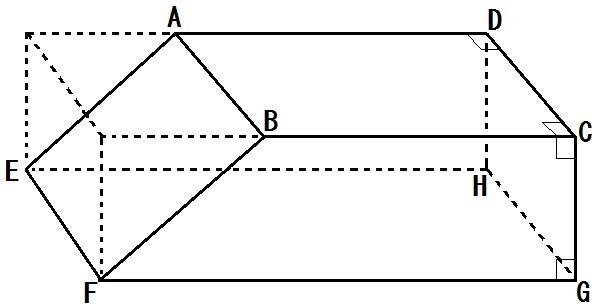



中学数学 空間図形 体積の問題のコツ
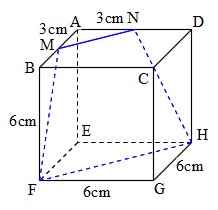



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




立派な 台形 体積 求め 方




小6算数 角柱 円柱の体積2 Youtube



台形の回転体 中学から数学だいすき



Xp9ax13dult21c0wtxqar30g7ld Com Saitama Sugaku R01 T Q8




立派な 台形 体積 求め 方



台形の形をした 立体の体積の求め方を知りたいのですがどなたか教えてくださ Yahoo 知恵袋




立派な 台形 体積 求め 方
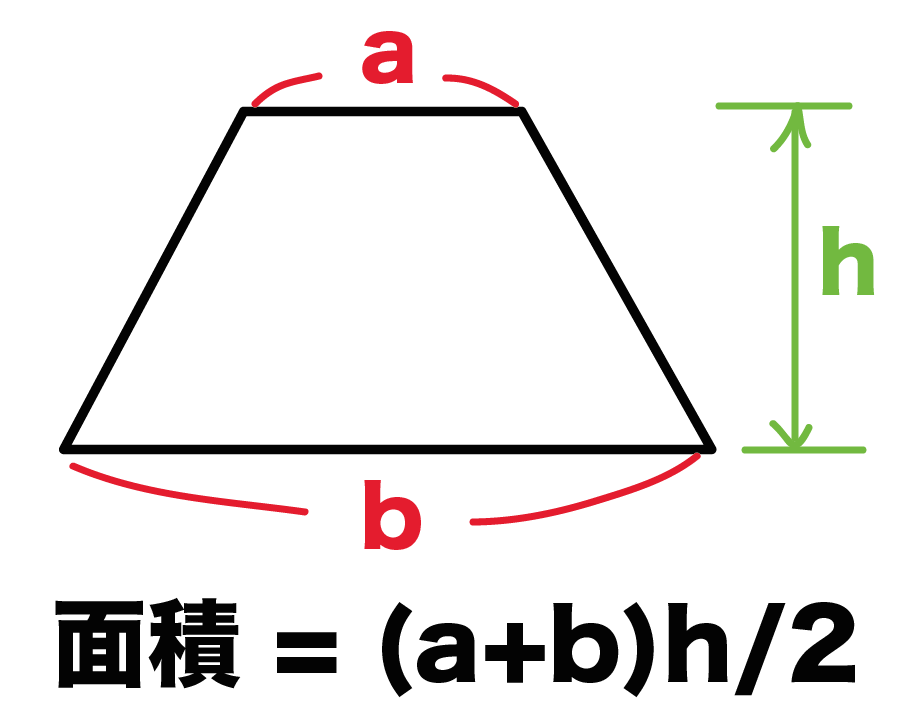



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿